题目内容
5.在一个不透明的袋子中,放有四张质地完全相同的卡片,分别标有数字1,2,3,4.第一次从袋中随机地抽出一张卡片,把其上的数字记为横坐标x,然后把卡片放回袋中,搅匀后第二次再随机地从中抽出一张,把其上的数字记为纵坐标y.(1)用树状图或列表法把所有可能的点表示出来;
(2)求所得的点在直线y=-x+5的点的概率.
分析 (1)此题需要两步完成,属于放回实验,所以采用树状图法或者采用列表法都比较简单,注意做到不重不漏;
(2)根据(1)求得所有的可情况,再求出符合条件的情况,即可求得答案.
解答 解:(1)树形图如下:
列表如下:
| (1,1) | (1,2) | (1,3) | (1,4) |
| (2,1) | (2,2) | (2,3) | (2,4) |
| (3,1) | (3,2) | (3,3) | (3,4) |
| (4,1) | (4,2) | (4,3) | (4,4) |
故P(所得的点在直线y=-x+5上)=$\frac{4}{16}$=$\frac{1}{4}$.
点评 此题考查了树状图与列表法求概率.列表法适合两步完成的事件,树状图法适合两步或两步以上完成的事件.解题时要注意此题是放回实验还是不放回实验.

练习册系列答案
相关题目
13.二元一次方程组$\left\{\begin{array}{l}{x+2y=1}\\{x-y=-2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ |
20.菱形ABCD的周长为16,∠A=60°,则BD的长为( )
| A. | 8 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
10.有A、B两个黑色袋子,A袋装有3个黑球、2个白球,B袋装有黑、白两个球,这些球除颜色外,其它一样.在随机抽球中,如果从A袋取一个球,再从B袋取一个球,那么得到两个都是黑球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{10}$ |
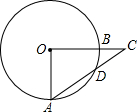 已知:如图,⊙O中,半径OA⊥OB,C是OB延长线上一点,AC交⊙O于D,若∠C=40°,求弧AD的度数.
已知:如图,⊙O中,半径OA⊥OB,C是OB延长线上一点,AC交⊙O于D,若∠C=40°,求弧AD的度数. 如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EFA,其中正确结论的序号是( )
如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EFA,其中正确结论的序号是( )