题目内容
 如图,⊙O的两条割线PAB交圆于A、B.割线PCD交圆于C、D.求证:(
如图,⊙O的两条割线PAB交圆于A、B.割线PCD交圆于C、D.求证:( |
| BD |
 |
| AC |
考点:圆心角、弧、弦的关系,圆周角定理
专题:证明题
分析:根据圆心角的度数等于它所对弧的度数和圆周角定理得到得到∠BCD等于
的度数的一半,∠ABC等于
的度数的一半,然后根据三角形外角性质进行证明.
 |
| BD |
 |
| AC |
解答: 证明:连结BC,如图,
证明:连结BC,如图,
∵∠BCD等于
的度数的一半,∠ABC等于
的度数的一半,
而∠BCD=∠P+∠PBC,
∴∠P=∠BCD-∠ABC,
∴∠P的度数等于
的度数的一半减去∠ABC等于
的度数的一半,
即
-
)的度数等于∠P度数的2倍.
 证明:连结BC,如图,
证明:连结BC,如图,∵∠BCD等于
 |
| BD |
 |
| AC |
而∠BCD=∠P+∠PBC,
∴∠P=∠BCD-∠ABC,
∴∠P的度数等于
 |
| BD |
 |
| AC |
即
 |
| BD |
 |
| AC |
点评:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了三角形外角性质和圆周周角定理.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
下列运算结果是负数的是( )
| A、(-5)+(-5) |
| B、(-5)-(-5) |
| C、(-5)*(-5) |
| D、(-5)÷(-5) |
 如图所示,根据图中信息,判断下列问题:
如图所示,根据图中信息,判断下列问题: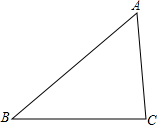 作图并解析:
作图并解析: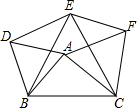 如图,已知△ABD,△BCE,△ACF都是等边三角形,试判断四边形ADEF的形状并说明理由.
如图,已知△ABD,△BCE,△ACF都是等边三角形,试判断四边形ADEF的形状并说明理由.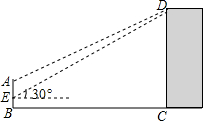 如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗,经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时测倾器离地面1.4m.求:
如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗,经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时测倾器离地面1.4m.求: