题目内容
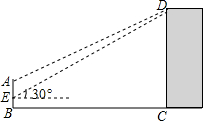 如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗,经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时测倾器离地面1.4m.求:
如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗,经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时测倾器离地面1.4m.求:(1)学校主楼的高度(结果精确到0.01m)
(2)大门顶部与主楼顶部的距离(结果精确到0.01m)
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:(1)过E做EN平行于BC交DC于N,利用三角函数求出ED的长;
(2)过A做AM平行于BC交DC于M,求出DM=DC-AB=13.72m,利用勾股定理求出AD的长.
(2)过A做AM平行于BC交DC于M,求出DM=DC-AB=13.72m,利用勾股定理求出AD的长.
解答: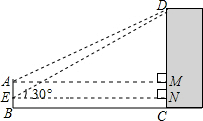 解:(1)过E做EN平行于BC交DC于N,
解:(1)过E做EN平行于BC交DC于N,
∠DEN=30°且BC=EN,
DN=EN•tan∠DEN=30•tan30°=10
m,
DC=DN+NC=DN+EB=10
+1.4≈18.72m.
(2)过A做AM平行于BC交DC于M,
∵DM=DC-MC且AB=DC,
∴DM=DC-AB=13.72m,
在Rt△AMD中∠AMD=90°,
∵AM=BC=30m,DM=13.72m,
由勾股定理得:
AD=
=
=32.99m.
答:学校主楼的高度为18.72米,大门顶部与主楼顶部的距离为32.99米.
 解:(1)过E做EN平行于BC交DC于N,
解:(1)过E做EN平行于BC交DC于N,∠DEN=30°且BC=EN,
DN=EN•tan∠DEN=30•tan30°=10
| 3 |
DC=DN+NC=DN+EB=10
| 3 |
(2)过A做AM平行于BC交DC于M,
∵DM=DC-MC且AB=DC,
∴DM=DC-AB=13.72m,
在Rt△AMD中∠AMD=90°,
∵AM=BC=30m,DM=13.72m,
由勾股定理得:
AD=
| MD2+AM2 |
| 13.722+302 |
答:学校主楼的高度为18.72米,大门顶部与主楼顶部的距离为32.99米.
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形,同时要熟悉勾股定理.

练习册系列答案
相关题目
 如图,⊙O的两条割线PAB交圆于A、B.割线PCD交圆于C、D.求证:(
如图,⊙O的两条割线PAB交圆于A、B.割线PCD交圆于C、D.求证:(
 如图,回答下列问题:
如图,回答下列问题: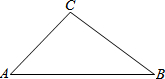 如图,在△ABC中,∠A=45°,AC=
如图,在△ABC中,∠A=45°,AC=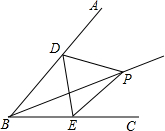 如图,已知点P是∠ABC的平分线与∠DEC的平分线的交点,求证:点P在∠ADE的平分线上.
如图,已知点P是∠ABC的平分线与∠DEC的平分线的交点,求证:点P在∠ADE的平分线上.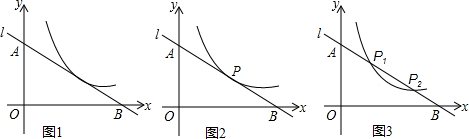
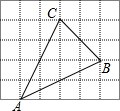 如图,网格中的每个小正方形的边长都是1,△ABC的每个顶点都在网格格点处,则sin∠CAB=
如图,网格中的每个小正方形的边长都是1,△ABC的每个顶点都在网格格点处,则sin∠CAB=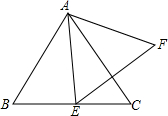 如图,点E为边长为4的等边△ABC的BC边上一动点(点E不与B、C重合),以AE为边作等边△AEF,求△AEF面积的最小值.
如图,点E为边长为4的等边△ABC的BC边上一动点(点E不与B、C重合),以AE为边作等边△AEF,求△AEF面积的最小值.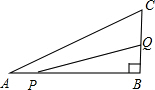 在△ABC中.∠B=90°,AB=6cm,BC=5cm,点P从点A开始,沿AB边向点B以1cm/s的速度移动,点Q从点B开始,沿BC边向点C以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发.经过多少秒后,△PBQ的面积等于8cm2?
在△ABC中.∠B=90°,AB=6cm,BC=5cm,点P从点A开始,沿AB边向点B以1cm/s的速度移动,点Q从点B开始,沿BC边向点C以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发.经过多少秒后,△PBQ的面积等于8cm2?