题目内容
4.解下列方程(或不等式)组,并把不等式组的解集表示在数轴上.(1)$\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{3}=2}\\{4x=y+5}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x-5<1+2x}\\{3x+2≤4x}\end{array}\right.$.
分析 (1)整理后①+②×2求出x,把x的值代入②求出y即可;
(2)先求出每个不等式的解集,再求出不等式组的解集即可.
解答 解:(1)整理得:$\left\{\begin{array}{l}{3x+2y=12①}\\{4x-y=5②}\end{array}\right.$
①+②×2得:11x=22,
解得:x=2,
把x=2代入②得:8-y=5,
解得:y=3,
所以原方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x-5<1+2x①}\\{3x+2≤4x②}\end{array}\right.$
∵解不等式①得:x>-6,
解不等式②得:x≥2,
∴不等式组的解集为x≥2,
在数轴上表示为: .
.
点评 本题考查了解一元一次不等式组,解二元一次方程组,在数轴上表示不等式组的解集等知识点,能把二元一次方程组转化成一元一次方程是解(1)的关键,能根据不等式的解集求出不等式组的解集是解(2)的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
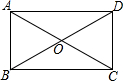 如图,在矩形ABCD中,AB=4,BC=6,点O为对角线交点,将矩形ABCD绕点O旋转,使得点B转至点A处,点C转至点E处.若AE,BC交于P点,则BP=$\frac{5}{3}$.
如图,在矩形ABCD中,AB=4,BC=6,点O为对角线交点,将矩形ABCD绕点O旋转,使得点B转至点A处,点C转至点E处.若AE,BC交于P点,则BP=$\frac{5}{3}$.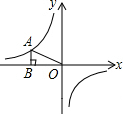 如图,点A是双曲线y=$\frac{-2}{x}$上一个动点,AB垂直于x轴,则△ABO的面积为1.
如图,点A是双曲线y=$\frac{-2}{x}$上一个动点,AB垂直于x轴,则△ABO的面积为1. 如图,直线l是一条河流,A、B是两个水库,现计划在河岸边修建一个水坝用于向A、B两个水库送水,要求水坝的位置点P到两个水库的距离相等,请用尺规在图中作出点P的位置.(不写作法,保留作图痕迹)
如图,直线l是一条河流,A、B是两个水库,现计划在河岸边修建一个水坝用于向A、B两个水库送水,要求水坝的位置点P到两个水库的距离相等,请用尺规在图中作出点P的位置.(不写作法,保留作图痕迹) 若关于x的不等式2x+a>-1的解集在数轴上表示如图,则a=3.
若关于x的不等式2x+a>-1的解集在数轴上表示如图,则a=3. 一个进水管和与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的函数关系如图所示.
一个进水管和与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的函数关系如图所示.