题目内容
15.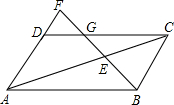 如图,?ABCD的边AD的延长线上取一点F,BF分别交AC,DC于点E,G,且EF=32cm,GF=18cm,求BE的长.
如图,?ABCD的边AD的延长线上取一点F,BF分别交AC,DC于点E,G,且EF=32cm,GF=18cm,求BE的长.
分析 首先设BE=xcm,然后由四边形ABCD是平行四边形,易证得△AFE∽△CBE,△DFG∽△CBG,然后由相似三角形的对应边成比例,证得$\frac{32}{x}$=$\frac{DF+AD}{BC}$=$\frac{DF}{BC}$+1,$\frac{DF}{BC}$=$\frac{18}{14+x}$,继而求得答案.
解答 解:设BE=xcm,
∵EF=32cm,GF=18cm,
∴GE=32-18=14,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,AB∥CD,
∴△AFE∽△CBE,
∴$\frac{EF}{BE}=\frac{AF}{BC}$,
∴$\frac{32}{x}$=$\frac{DF+AD}{BC}$=$\frac{DF}{BC}$+1,
∵DG∥AB,
∴△DFG∽△CBG,
∴$\frac{DF}{BC}$=$\frac{FG}{BG}$,
∴$\frac{DF}{BC}$=$\frac{18}{14+x}$,
∴$\frac{32}{x}$-1=$\frac{18}{14+x}$,
解得:x=±8$\sqrt{7}$(负数舍去),
故BE=8$\sqrt{7}$cm.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质.注意证得△AFE∽△CBE,△DFG∽△CBG,从而得到方程$\frac{32}{x}$-1=$\frac{18}{14+x}$是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
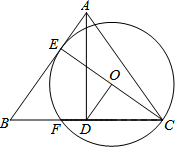 如图,在△ABC中,AB=AC,AD⊥BC于点D,过点C作⊙O与边AB相切于点E,交BC于点F,CE为⊙O的直径.
如图,在△ABC中,AB=AC,AD⊥BC于点D,过点C作⊙O与边AB相切于点E,交BC于点F,CE为⊙O的直径. 如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.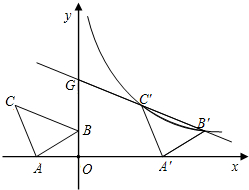 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2). 如图,一只松鼠在树干的A处,从地面C测得AC的距离是6m,仰角是43°,1s后,松鼠跳到B处,此时测得BC的距离是6.13m,仰角为45.54°,解答下列问题
如图,一只松鼠在树干的A处,从地面C测得AC的距离是6m,仰角是43°,1s后,松鼠跳到B处,此时测得BC的距离是6.13m,仰角为45.54°,解答下列问题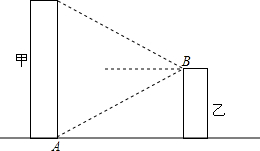 某城市搞亮化工程,如图,在甲楼底部,乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.
某城市搞亮化工程,如图,在甲楼底部,乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.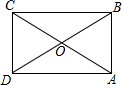 如图,在矩形ABCD中,对角线AC、BD相交于点O,OA=AB,OD=3cm,则矩形ABCD的面积为9$\sqrt{3}$cm2.
如图,在矩形ABCD中,对角线AC、BD相交于点O,OA=AB,OD=3cm,则矩形ABCD的面积为9$\sqrt{3}$cm2.