题目内容
5.若点M、N是一次函数y1=-x+5与反比例函数y2=$\frac{k}{x}$(k≠0,x>0)图象的两个交点,其中点M的横坐标为1,下列结论:①一次函数y1=-x+5的图象不经过第三象限;②点N的纵坐标为1;③若将一次函数y1=-x+5的图象向下平移1个单位,则与反比例函数y2=$\frac{k}{x}$(k≠0,x>0)图象有且只有一个交点;④当1<x<4时,y1<y2.其中结论正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据一次函数的性质即可判断①;利用待定系数法求得M的坐标,进而求得N的坐标,即可判断②;求得直线向下平移后的解析式,然后联立方程求得交点坐标即可判断③;根据函数的图象结合交点坐标即可判断④.
解答 解:由一次函数y1=-x+5可知,一次函数y1=-x+5的图象经过第一、二、四象限,不经过第三象限;
故①正确;
∵点M的横坐标为1,
∴y=-1+5=4,
∴M(1,4),
∴k=4,
∴反比例函数y2=$\frac{4}{x}$(k≠0,x>0),
解$\left\{\begin{array}{l}{y=-x+5}\\{y=\frac{4}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,
∴N的纵坐标为1,
故②正确;
将一次函数y1=-x+5的图象向下平移1个单位长度,则函数的解析式为y=-x+4,
解$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{4}{x}}\end{array}\right.$解得$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=2}\end{array}\right.$,
∴将一次函数y1=-x+5的图象向下平移1个单位,则与反比例函数y2=$\frac{k}{x}$(k≠0,x>0)图象有且只有一个交点;
故③正确;
∵M(1,4),N(4,1),根据图象可知当1<x<4时,一次函数图象部分在反比例函数图象的上方,所以y1>y2.
故④错误.
故选B.
点评 本题考查了一次函数和二次函数的交点坐标,其知识点有:待定系数法求解析式,平移的性质以及交点的求法等.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案| 购买苹果数量 | 不超过30千克 | 超30千克但不超过50千克 | 50千克以上 |
| 每千克价格/元 | 3元 | 2.5元 | 2元 |
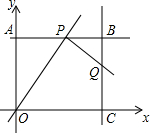 如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.
如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q. 如图,矩形对角线AC,BD相交于点O,∠AOB=60°,AB=4cm,求矩形对角线AC和BC的长.
如图,矩形对角线AC,BD相交于点O,∠AOB=60°,AB=4cm,求矩形对角线AC和BC的长.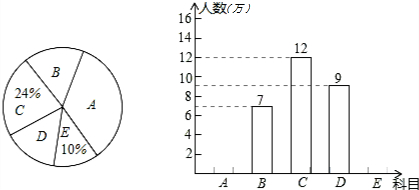 园;D:明月岛,E:青年林场.市旅游局对某月进入景点的人数情况进行调查统计,制成了两幅不完整的统计图(如图).
园;D:明月岛,E:青年林场.市旅游局对某月进入景点的人数情况进行调查统计,制成了两幅不完整的统计图(如图).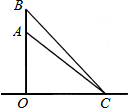 如图,一只松鼠在树干的A处,从地面C测得AC的距离是6m,仰角是43°,1s后,松鼠跳到B处,此时测得BC的距离是6.13m,仰角为45.54°,解答下列问题
如图,一只松鼠在树干的A处,从地面C测得AC的距离是6m,仰角是43°,1s后,松鼠跳到B处,此时测得BC的距离是6.13m,仰角为45.54°,解答下列问题 如图,∠B=∠C,AB=AC,△ABE与△ACD全等吗?为什么?
如图,∠B=∠C,AB=AC,△ABE与△ACD全等吗?为什么? 如图,△ABC≌△FED且BC=DE,问AB∥EF吗?请说明理由.
如图,△ABC≌△FED且BC=DE,问AB∥EF吗?请说明理由.