题目内容
14.已知有9张卡片,分别写有1到9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则使关于x的不等式组$\left\{\begin{array}{l}{4x≥3(x+1)}\\{2x-\frac{x-1}{2}<a}\end{array}\right.$有解的概率为( )| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
分析 根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
解答 解:因为关于x的不等式组$\left\{\begin{array}{l}{4x≥3(x+1)}\\{2x-\frac{x-1}{2}<a}\end{array}\right.$有解,
可得:$\left\{\begin{array}{l}{x≥3}\\{x<\frac{2}{3}(a-\frac{1}{2})}\end{array}\right.$,
所以得出a>5,
因为a取≤9的整数,
可得a的可能值为6,7,8,9,共4种可能性,
所以使关于x的不等式组$\left\{\begin{array}{l}{4x≥3(x+1)}\\{2x-\frac{x-1}{2}<a}\end{array}\right.$有解的概率为$\frac{4}{9}$,
故选C
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
5.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 等腰三角形 | B. | 平行四边形 | C. | 梯形 | D. | 圆 |
2.先化简,再求值:$\frac{4a}{{a}^{2}-4a+4}$÷$\frac{{a}^{2}+2a}{{a}^{2}-4}$-$\frac{1}{a-2}$,其中a=$\sqrt{3}$+2.
4. 小亮和小明周六到距学校24km的滨湖湿地公园春游,小亮8:00从学校出发,骑自行车去湿地公园,小明8:30从学校出发,乘车沿相同路线去滨湖湿地公园,在同一直角坐标系中,小亮和小明的行进路程S(km)与时间t(时)的函数图象如图所示.根据图象得到结论,其中错误的是( )
小亮和小明周六到距学校24km的滨湖湿地公园春游,小亮8:00从学校出发,骑自行车去湿地公园,小明8:30从学校出发,乘车沿相同路线去滨湖湿地公园,在同一直角坐标系中,小亮和小明的行进路程S(km)与时间t(时)的函数图象如图所示.根据图象得到结论,其中错误的是( )
 小亮和小明周六到距学校24km的滨湖湿地公园春游,小亮8:00从学校出发,骑自行车去湿地公园,小明8:30从学校出发,乘车沿相同路线去滨湖湿地公园,在同一直角坐标系中,小亮和小明的行进路程S(km)与时间t(时)的函数图象如图所示.根据图象得到结论,其中错误的是( )
小亮和小明周六到距学校24km的滨湖湿地公园春游,小亮8:00从学校出发,骑自行车去湿地公园,小明8:30从学校出发,乘车沿相同路线去滨湖湿地公园,在同一直角坐标系中,小亮和小明的行进路程S(km)与时间t(时)的函数图象如图所示.根据图象得到结论,其中错误的是( )| A. | 小亮骑自行车的平均速度是12km/h | |
| B. | 小明比小亮提前0.5小时到达滨湖湿地公园 | |
| C. | 小明在距学校12km处追上小亮 | |
| D. | 9:30小明与小亮相距4km |
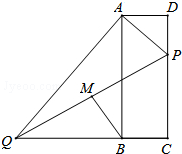 如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.