题目内容
 函数y=x2+bx+c与y=x的图象如图所示,下面结论:①b2-4c>0,②b+c+1=0,③3b+c+6=0,④当1<x<3时,x2+(b-1)x+c<0,其中正确的是( )
函数y=x2+bx+c与y=x的图象如图所示,下面结论:①b2-4c>0,②b+c+1=0,③3b+c+6=0,④当1<x<3时,x2+(b-1)x+c<0,其中正确的是( )| A、②③④ | B、③④ |
| C、①②③④ | D、① |
考点:二次函数图象与系数的关系
专题:
分析:由函数y=x2+bx+c与x轴无交点,可得b2-4c<0;当x=1时,y=1+b+c=1;当x=3时,y=9+3b+c=3;当1<x<3时,二次函数值小于一次函数值,可得x2+bx+c<x,继而可求得答案.
解答:解:∵函数y=x2+bx+c与x轴无交点,
∴b2-4c<0;
故①错误;
当x=1时,y=1+b+c=1,
故②错误;
∵当x=3时,y=9+3b+c=3,
∴3b+c+6=0;
故③正确;
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b-1)x+c<0.
故④正确.
故选B.
∴b2-4c<0;
故①错误;
当x=1时,y=1+b+c=1,
故②错误;
∵当x=3时,y=9+3b+c=3,
∴3b+c+6=0;
故③正确;
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b-1)x+c<0.
故④正确.
故选B.
点评:本题考查了图象与二次函数系数之间的关系.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
-2014的相反数是( )
| A、2014 | ||
B、
| ||
C、-
| ||
| D、-2014 |
 如图,在△ABC中,∠B=40°,∠C=110°.按要求完成下列各题.
如图,在△ABC中,∠B=40°,∠C=110°.按要求完成下列各题. 二次函数y=-x2+bx+c的图象如图所示,试确定b、c的符号:b
二次函数y=-x2+bx+c的图象如图所示,试确定b、c的符号:b 如图,平行四边形ABCD纸片中,AC⊥AB,AC与BD交于点O,沿对角线AC对折后,E与B对应.
如图,平行四边形ABCD纸片中,AC⊥AB,AC与BD交于点O,沿对角线AC对折后,E与B对应.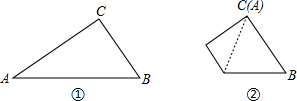 如图,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C重合(如图②);
如图,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C重合(如图②); 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上. 如图,△ABC中AB=AC,∠ABC=45°,AD⊥BC,⊙O经过A,B,D三点,求证:AC是⊙O的切线.
如图,△ABC中AB=AC,∠ABC=45°,AD⊥BC,⊙O经过A,B,D三点,求证:AC是⊙O的切线. 在?ABCD中,对角线AC=8,BD=6,AC和BD的夹角为α,当α=45°时,?ABCD的面积为
在?ABCD中,对角线AC=8,BD=6,AC和BD的夹角为α,当α=45°时,?ABCD的面积为