题目内容
 二次函数y=-x2+bx+c的图象如图所示,试确定b、c的符号:b
二次函数y=-x2+bx+c的图象如图所示,试确定b、c的符号:b考点:二次函数图象与系数的关系
专题:
分析:由抛物线的对称轴在y轴左侧得出a与b同号,又a=-1<0,则b<0;由抛物线与y轴的交点在x轴上方,得出c>0.
解答:解:∵抛物线的对称轴在y轴左侧,
∴a与b符号相同,
又a=-1<0,
∴b<0;
∵抛物线与y轴的交点在x轴上方,
∴c>0.
故答案为<,>.
∴a与b符号相同,
又a=-1<0,
∴b<0;
∵抛物线与y轴的交点在x轴上方,
∴c>0.
故答案为<,>.
点评:本题考查了二次函数y=ax2+bx+c(a≠0)的图象与系数的关系:
①二次项系数a决定抛物线的开口方向和大小.
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;
②一次项系数b和二次项系数a共同决定对称轴的位置.
当a与b同号时(即ab>0),对称轴在y轴左侧; 当a与b异号时(即ab<0),对称轴在y轴右侧(简称:左同右异);
③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).
④抛物线与x轴交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.
①二次项系数a决定抛物线的开口方向和大小.
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;
②一次项系数b和二次项系数a共同决定对称轴的位置.
当a与b同号时(即ab>0),对称轴在y轴左侧; 当a与b异号时(即ab<0),对称轴在y轴右侧(简称:左同右异);
③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).
④抛物线与x轴交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
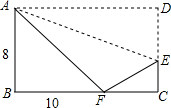 如图,在平面直角坐标系中放入一张长方形纸片ABCD,其中B是坐标原点,BC,AB分别在x轴、y轴的正半轴上,现将纸片沿AE翻折,使点D落在x轴上,记为F,若AB=8,BC=10,则E点的坐标为( )
如图,在平面直角坐标系中放入一张长方形纸片ABCD,其中B是坐标原点,BC,AB分别在x轴、y轴的正半轴上,现将纸片沿AE翻折,使点D落在x轴上,记为F,若AB=8,BC=10,则E点的坐标为( )| A、(10,4) |
| B、(10,3) |
| C、(6,4) |
| D、(6,3) |

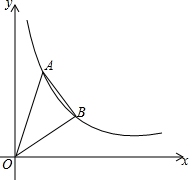 如图,在平面直角坐标系中,直线y=4x、y=x分别与双曲线y=
如图,在平面直角坐标系中,直线y=4x、y=x分别与双曲线y= 函数y=x2+bx+c与y=x的图象如图所示,下面结论:①b2-4c>0,②b+c+1=0,③3b+c+6=0,④当1<x<3时,x2+(b-1)x+c<0,其中正确的是( )
函数y=x2+bx+c与y=x的图象如图所示,下面结论:①b2-4c>0,②b+c+1=0,③3b+c+6=0,④当1<x<3时,x2+(b-1)x+c<0,其中正确的是( ) 如图,AB∥CD,OB⊥AB,∠D=120°,则∠O=
如图,AB∥CD,OB⊥AB,∠D=120°,则∠O= 如图,∠AOB等于∠COD,请判断∠AOC和∠BOD的大小关系并说明理由.
如图,∠AOB等于∠COD,请判断∠AOC和∠BOD的大小关系并说明理由.