题目内容
19.已知:抛物线y=-x2-2x+1,(1)求出它的顶点坐标;请问函数有最大值还是最小值?求出最值;
(2)若抛物线的顶点在双曲线$y=\frac{k}{x}$上,求出k值.
分析 (1)将抛物线y=-x2-2x+1化为顶点式,即可得到该函数的顶点坐标,由a=-1<0,可知该抛物线有最大值,根据顶点式可以直接得到该函数的最大值;
(2)由(1)中求得的顶点坐标和抛物线的顶点在双曲线$y=\frac{k}{x}$上,可以求得k的值.
解答 解:(1)∵y=-x2-2x+1=-(x2+2x)+1=-(x+1)2+2,
∴抛物线的顶点坐标是(-1,2),该函数有最大值,最大值是2;
(2)∵抛物线的顶点坐标是(-1,2),抛物线的顶点在双曲线$y=\frac{k}{x}$上,
∴2=$\frac{k}{-1}$,
解得,k=-2.
点评 本题考查二次函数的最值,解题的关键是可以将二次函数的一般式化为顶点式,明确二次函数的性质.

练习册系列答案
相关题目
8.下图是上海今年春节七天最高气温(℃)的统计结果:
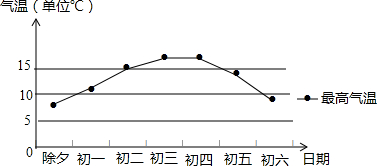
这七天最高气温的众数和中位数是( )

这七天最高气温的众数和中位数是( )
| A. | 15,17 | B. | 14,17 | C. | 17,14 | D. | 17,15 |
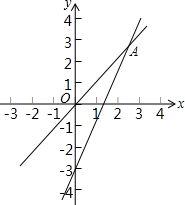 已知一个正比例函数与一个一次函数的图象交于点A(3,4),且0A=0B
已知一个正比例函数与一个一次函数的图象交于点A(3,4),且0A=0B
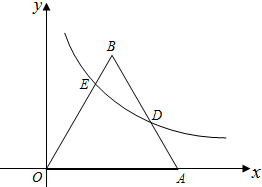 如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过AB边的中点D,交OB边于点E.
如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过AB边的中点D,交OB边于点E.