题目内容
15.二次函数y=ax2+bx+1(a≠0)与一次函数y=ax+1(a≠0)在同一直角坐标系中的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据二次函数和一次函数图象的特点,可知两个函数都过点(0,1),从而可以判断B、C错误,然后再判断A、D即可.
解答 解:由二次函数y=ax2+bx+1(a≠0)与一次函数y=ax+1(a≠0)可得,两个函数都过点(0,1),故选项B、C错误;
在A和D两个选项中,由一次函数y=ax+1(a≠0)过一、二、四象限可知a<0,则二次函数y=ax2+bx+1开口向下,故A正确,D错误;
故选A.
点评 本题考查二次函数和一次函数的图象,解题的关键是明确一次函数图象和二次函数图象的特点,利用数形结合的思想解答.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
6. (1)画出函数y=-$\frac{6}{x}$(x<0)的图象:
(1)画出函数y=-$\frac{6}{x}$(x<0)的图象:
列表:
描点并连线.
(2)从图象可以看出,曲线从左向右依次升高,当x由小变大时,y=-$\frac{6}{x}$(x<0)随之变大.
 (1)画出函数y=-$\frac{6}{x}$(x<0)的图象:
(1)画出函数y=-$\frac{6}{x}$(x<0)的图象:列表:
| x | … | -6 | -5 | -4 | -3 | -2 | -1 | … |
| y | … | … |
(2)从图象可以看出,曲线从左向右依次升高,当x由小变大时,y=-$\frac{6}{x}$(x<0)随之变大.
3.若直线y=kx+b(k<0,b>0)的大致图象为( )
| A. |  | B. |  | C. |  | D. |  |
20. 如图,在平面直角坐标系中,OA⊥OB,sin∠OAB=$\frac{1}{2}$,点A、B分别在反比例函数y1=$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上,则k的值是( )
如图,在平面直角坐标系中,OA⊥OB,sin∠OAB=$\frac{1}{2}$,点A、B分别在反比例函数y1=$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上,则k的值是( )
 如图,在平面直角坐标系中,OA⊥OB,sin∠OAB=$\frac{1}{2}$,点A、B分别在反比例函数y1=$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上,则k的值是( )
如图,在平面直角坐标系中,OA⊥OB,sin∠OAB=$\frac{1}{2}$,点A、B分别在反比例函数y1=$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上,则k的值是( )| A. | -$\frac{2}{3}$ | B. | -$\frac{2\sqrt{3}}{3}$ | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
5.截止到目前,参加北京市普通小客车摇号的申请人数已经超过2500000人,将2500000用科学记数法表示为( )
| A. | 25×10 5 | B. | 2.5×106 | C. | 0.25×10 7 | D. | 2.5×108 |
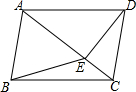 如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
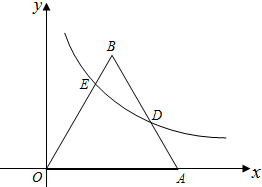 如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过AB边的中点D,交OB边于点E.
如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过AB边的中点D,交OB边于点E.