题目内容
12．
已知一次函数y=2x-6，（1）画出该函数的图象．
（2）判断（4，3）是否在此函数的图象上．
（3）观察画出的图象，说一说当x为何值时y＜0？
分析 （1）求值直线与坐标轴的交点，画出函数图象即可；
（2）把（4，3）代入函数解析式检验即可；
（3）根据函数图象即可得出结论．
解答 
解：（1）∵一次函数y=2x-6与坐标轴的交点为（0，-6），（3，0），
∴函数图象如图；
（2）∵当x=4时，y=8-6=2≠3，
∴该点不在图象上；
（3）由图可知，当x＜3时，y＜0．
点评 本题考查的是一次函数的图象，能利用函数图象直接求出不等式的解集是解答此题的关键．
练习册系列答案
相关题目
3．若直线y=kx+b（k＜0，b＞0）的大致图象为（ ）
| A． |  | B． |  | C． |  | D． |  |
20．
如图，在平面直角坐标系中，OA⊥OB，sin∠OAB=$\frac{1}{2}$，点A、B分别在反比例函数y1=$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上，则k的值是（ ）
如图，在平面直角坐标系中，OA⊥OB，sin∠OAB=$\frac{1}{2}$，点A、B分别在反比例函数y1=$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上，则k的值是（ ）| A． | -$\frac{2}{3}$ | B． | -$\frac{2\sqrt{3}}{3}$ | C． | -2$\sqrt{3}$ | D． | 2$\sqrt{3}$ |
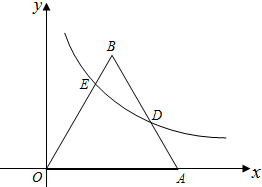如图，等边△ABO在平面直角坐标系中，点A的坐标为（4，0），函数y=$\frac{k}{x}$（x＞0，k是常数）的图象经过AB边的中点D，交OB边于点E．
