在直角三角形ABC中.已知直角边a=$\sqrt{96}$.斜边c=$\sqrt{150}$.求△ABC的面积．题目和参考答案——青夏教育精英家教网—

题目内容

12．在直角三角形ABC中，已知直角边a=$\sqrt{96}$，斜边c=$\sqrt{150}$，求△ABC的面积．

分析首先利用勾股定理求得另一条直角边b，进一步利用三角形的面积计算公式求得答案即可．

解答解：另一条直角边b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{150-96}$=3$\sqrt{6}$；
△ABC的面积=$\frac{1}{2}$ab=$\frac{1}{2}$×$\sqrt{96}$×3$\sqrt{6}$=$\frac{1}{2}$×4$\sqrt{6}$×3$\sqrt{6}$=36．

点评此题考查二次根式的实际运用，掌握勾股定理，三角形的面积计算公式是解决问题的关键．

练习册系列答案

3．已知A（1，0），B（3，1），△ABC是等腰直角三角形时，点C的坐标为（0，2），（2，3），（2，-2），（4，-1），（$\frac{3}{2}$，$\frac{3}{2}$），（$\frac{1}{2}$，-$\frac{5}{2}$）．

20．

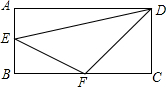如图，矩形ABCD中，AB=6，BC=12，E是AB上一点，F是BC上一点，且BF=2BE．设BE=x，△DEF的面积为S，则S关于x的函数关系式为-x²+12x（0＜x＜6）．

7．如图，△0AB与△ODC是位似图形，试问：

（1）AB与CD平行吗？请说明理由；
（2）如果OB=3，OC=4，OD=3.5，试求△OAB与△ODC的相似比及OA的长．

17．找规律填数：4、-16、36、-64、100、-144、196．

4．计算：
（1）（1$\frac{3}{4}$-$\frac{7}{8}$-$\frac{7}{12}$）÷（-$\frac{7}{8}$）+（-$\frac{8}{3}$）；
（2）[-21⁴-（-2）⁵+（-21）⁴]×[-$\frac{5}{3}$×$\frac{8}{15}$×（-$\frac{1}{4}$）×9-6²]÷32；
（3）[47-（18.75-1÷$\frac{8}{15}$）×2$\frac{6}{25}$]÷0.46．

6．轴对称在数学计算中有巧妙的应用．如图①，现要计算长方形中六个数字的和，我们发现，把长方形沿对称轴l₁对折，重合的数字均为4，故六个数字的和为3×4=12，若沿对称轴l₂对折，则六个数字的和可表示为4×2+2×2=12，受上面方法的启发，请快速计算长方形（图②）中各数字之和．

7．如图，将一副直角三角板的直角顶点C叠放一起．
（1）如图1，若CE恰好是∠ACB的角平分线，请你猜想此时CB是不是∠ECD的角平分线？并简述理由．
（2）如图2，若CB始终在∠DCE的内部，请猜想∠ACE与∠DCB是否相等？并简述理由．
（3）如图2，若CB始终在∠CDE的内部，设∠BCE=β，试用含β的代数式表示∠ACD的度数，并说明当β的值增大时，∠ACD的大小会发生怎样的变化？

试题分类