题目内容
7.如图,△0AB与△ODC是位似图形,试问: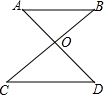
(1)AB与CD平行吗?请说明理由;
(2)如果OB=3,OC=4,OD=3.5,试求△OAB与△ODC的相似比及OA的长.
分析 (1)首先根据位似图形的性质可判定△OAB和△ODC相似,再根据相似三角形的性质可判断∠A和∠D的关系,最后根据平行线的判断即可得AB平行于CD;
(2)直接利用相似三角形的判定与性质得出$\frac{AO}{DO}$=$\frac{BO}{CO}$,进而得出答案.
解答 解:(1)AB∥CD;
理由如下:
∵△OAB与△ODC是位似图形,
∴△OAB∽△ODC,
∴∠A=∠D,
∴AB∥CD(内错角相等,两直线平行);
(2)∵△OAB∽△ODC,
∴$\frac{AO}{DO}$=$\frac{BO}{CO}$,
∴$\frac{AO}{3.5}$=$\frac{3}{4}$,
解得:AO=$\frac{21}{8}$.
点评 此题主要考查了位似图形的性质以及相似三角形的判定与性质,正确利用相似三角形性质求出是解题关键.

练习册系列答案
相关题目
 如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=57°,求∠CAD的度数.
如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=57°,求∠CAD的度数.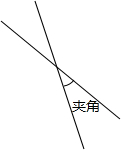 两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问:
两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问: