题目内容
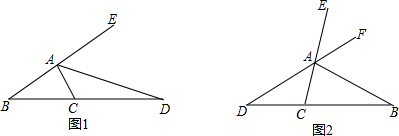
7.如图,将一副直角三角板的直角顶点C叠放一起.(1)如图1,若CE恰好是∠ACB的角平分线,请你猜想此时CB是不是∠ECD的角平分线?并简述理由.
(2)如图2,若CB始终在∠DCE的内部,请猜想∠ACE与∠DCB是否相等?并简述理由.
(3)如图2,若CB始终在∠CDE的内部,设∠BCE=β,试用含β的代数式表示∠ACD的度数,并说明当β的值增大时,∠ACD的大小会发生怎样的变化?
分析 (1)根据角平分线的定义求出∠ECB=45°,计算即可证明;
(2)根据图形和同角的余角相等解答;
(3)根据∠ACD=90°+90°-∠BCE计算即可.
解答 解:(1)CB是∠ECD的角平分线,
∵∠ACB=90°,CE恰好是∠ACB的角平分线,
∴∠ECB=45°,
∴∠DCB=90°-45°=45°,
∴∠ECB=∠DCB,
∴CB是∠ECD的角平分线;
(2)∠ACE=∠DCB,
∵∠ACE+∠ECB=90°,∠DCB+∠ECB=90°,
∴∠ACE=∠DCB;
(3)∠ACD=90°+90°-∠BCE=180°-β,
当β的值增大时,∠ACD的度数逐渐减小.
点评 本题考查的是角的计算,能够根据图形结合角平分线的性质进行角的计算是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
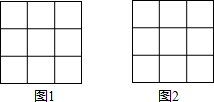 如图,在3×3的正方形网格中,每个小正方形的边长都是1,每个小格的顶点叫格点,以格点为顶点,分别按下列要求画三角形:
如图,在3×3的正方形网格中,每个小正方形的边长都是1,每个小格的顶点叫格点,以格点为顶点,分别按下列要求画三角形: 如图,△ABC中,∠BAC=120°,∠ABC=15°,∠A,∠B,∠C的对边分别是a,b,c,则a:b:c=2$\sqrt{3}$:($\sqrt{6}$-$\sqrt{2}$):2$\sqrt{2}$.
如图,△ABC中,∠BAC=120°,∠ABC=15°,∠A,∠B,∠C的对边分别是a,b,c,则a:b:c=2$\sqrt{3}$:($\sqrt{6}$-$\sqrt{2}$):2$\sqrt{2}$.