题目内容
20.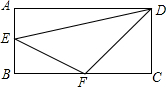 如图,矩形ABCD中,AB=6,BC=12,E是AB上一点,F是BC上一点,且BF=2BE.设BE=x,△DEF的面积为S,则S关于x的函数关系式为-x2+12x(0<x<6).
如图,矩形ABCD中,AB=6,BC=12,E是AB上一点,F是BC上一点,且BF=2BE.设BE=x,△DEF的面积为S,则S关于x的函数关系式为-x2+12x(0<x<6).
分析 由矩形的性质得出∠A=∠B=∠C=90°,CD=AB=6,AD=BC=12,由BE=x,得出BF=2BE=2x,AE=6-x,CF=12-x,△DEF的面积=矩形ABCD的面积-△BEF的面积-△CDF的面积-△ADE的面积,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,CD=AB=6,AD=BC=12,
∵BE=x,则BF=2BE=2x,AE=6-x,CF=12-x,
∵△DEF的面积=矩形ABCD的面积-△BEF的面积-△CDF的面积-△ADE的面积
=12×6-$\frac{1}{2}$•2x•x-$\frac{1}{2}$×6(12-2x)-$\frac{1}{2}$×12(6-x)
=-x2+12x,
∴S=-x2+12x(0<x<6).
故答案为:-x2+12x(0<x<6).
点评 本题考查了矩形的性质、三角形面积的计算方法;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列说法错误的是( )
| A. | 一个非零数与其倒数之积为1 | |
| B. | 一个数与其相反数之商为-1 | |
| C. | 若两个数的商为-1,则这两个数互为相反数 | |
| D. | 若两个数的积为1,则这两个数互为倒数 |
 如图,△AOB≌△DOC,△AOB的周长为10,且BC=4,则△DBC的周长为14.
如图,△AOB≌△DOC,△AOB的周长为10,且BC=4,则△DBC的周长为14. 如图是一个长与宽之比为2:1的长方形草坪,其对角线长为$\sqrt{125}$米,现欲改造成一个面积相等的正方形草坪,则改造后的正方形草坪的边长为5$\sqrt{2}$米.
如图是一个长与宽之比为2:1的长方形草坪,其对角线长为$\sqrt{125}$米,现欲改造成一个面积相等的正方形草坪,则改造后的正方形草坪的边长为5$\sqrt{2}$米.
 如图,△ABC中,∠BAC=120°,∠ABC=15°,∠A,∠B,∠C的对边分别是a,b,c,则a:b:c=2$\sqrt{3}$:($\sqrt{6}$-$\sqrt{2}$):2$\sqrt{2}$.
如图,△ABC中,∠BAC=120°,∠ABC=15°,∠A,∠B,∠C的对边分别是a,b,c,则a:b:c=2$\sqrt{3}$:($\sqrt{6}$-$\sqrt{2}$):2$\sqrt{2}$.