题目内容
7.阅读材料:对于任何实数,我们规定符号“$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$”称为二阶行列式,规定它的运算法则为:$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc.(1)按照这个规定请你计算$|\begin{array}{l}{5}&{6}\\{7}&{-8}\end{array}|$的值;
(2)请你根据上述规定求出等式$|\begin{array}{l}{2}&{1}\\{\frac{1}{1-x}}&{\frac{1}{x-1}}\end{array}|$=1中x的值.
分析 (1)原式利用题中的新法则计算即可得到结果;
(2)已知等式利用题中的新法则变形,求出解即可得到x的值.
解答 解:(1)根据题中新法则得:原式=5×(-8)-7×6=-40-42=-82;
(2)由题意得:2×$\frac{1}{x-1}$-$\frac{1}{1-x}$=1,即$\frac{2}{x-1}$+$\frac{1}{x-1}$=1,
去分母得:3=x-1,
解得:x=4,
检验:当x=4时,x-1≠0,
∴x=4为原方程的解.
∴x的值为4.
点评 此题考查了解分式方程,弄清题中的新法则是解本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
18.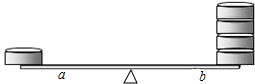 如图,用一根质地均匀的直尺和一些棋子做实验:在直尺的一端放一枚棋子.另一端放n枚棋子,移动质点的位置,使两边平衡,记录支点到两端的距离a,b,如下表:
如图,用一根质地均匀的直尺和一些棋子做实验:在直尺的一端放一枚棋子.另一端放n枚棋子,移动质点的位置,使两边平衡,记录支点到两端的距离a,b,如下表:
(1)根据统计记录,你发现的规律是a=nb;
(2)若直尺长60cm,直尺的一端放一枚棋子,另一端放9枚棋子,试用一元一次方程求出a,b的值.
 如图,用一根质地均匀的直尺和一些棋子做实验:在直尺的一端放一枚棋子.另一端放n枚棋子,移动质点的位置,使两边平衡,记录支点到两端的距离a,b,如下表:
如图,用一根质地均匀的直尺和一些棋子做实验:在直尺的一端放一枚棋子.另一端放n枚棋子,移动质点的位置,使两边平衡,记录支点到两端的距离a,b,如下表:| n(枚) | 1 | 2 | 3 | 4 | 5 |
| a/cm | 15 | 20 | 22.5 | 24 | 25 |
| b/cm | 15 | 10 | 7.5 | 6 | 5 |
(2)若直尺长60cm,直尺的一端放一枚棋子,另一端放9枚棋子,试用一元一次方程求出a,b的值.
2.计算(-$\frac{1}{4}$)-2的结果为( )
| A. | $-\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{16}$ | D. | 16 |
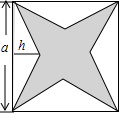 如图,一个正方形剪去四个相同的三角形,已知正方形的边长为a,三角形的高为h
如图,一个正方形剪去四个相同的三角形,已知正方形的边长为a,三角形的高为h