题目内容
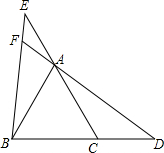
5. 如图,在△ABC中,AB=AC=2,∠A=90°,点P为BC的中点,点E、F分别为边AB、AC上的点,若∠EPF=45°,∠FEP=60°,则CF=3-$\sqrt{3}$.
如图,在△ABC中,AB=AC=2,∠A=90°,点P为BC的中点,点E、F分别为边AB、AC上的点,若∠EPF=45°,∠FEP=60°,则CF=3-$\sqrt{3}$.
分析 由等腰直角三角形的性质求得∠B=∠C=45°;然后由三角形内角和定理、邻补角的定义求得∠BPE=∠CFP,证得△BPE∽△CFP;过点F作EM⊥EP于点M,设EM=a,求出FM=$\sqrt{3}$a、PM=$\sqrt{3}$a、FP=$\sqrt{6}$a,得$\frac{EP}{PF}=\frac{1+\sqrt{3}}{\sqrt{6}}$,再利用相似三角形对应边成比例可得CF长.
解答 解:如图,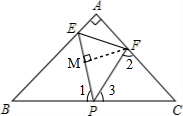
∵在△ABC中,AB=AC=2,∠A=90°,
∴∠B=∠C=45°,BP=CP=$\frac{1}{2}$BC=$\sqrt{2}$,
∴∠2+∠3=135°.
又∵∠EPF=45°
∴∠1+∠3=135°
∴∠1=∠2,
∴△BPE∽△CFP.
过点F作EM⊥EP于点M,设EM=a.
在Rt△EMF中,∵∠FEP=60°,
∴FM=$\sqrt{3}$a,
在Rt△FMP中,得到PM=$\sqrt{3}$a,FP=$\sqrt{6}$a,
则$\frac{EP}{PF}=\frac{a+\sqrt{3}a}{\sqrt{6}a}=\frac{1+\sqrt{3}}{\sqrt{6}}$,
∵△BPE∽△CFP,
∴$\frac{BP}{CF}=\frac{EP}{PF}$,即$\frac{\sqrt{2}}{CF}=\frac{1+\sqrt{3}}{\sqrt{6}}$,
解得:CF=3-$\sqrt{3}$.
故答案为:3-$\sqrt{3}$.
点评 本题主要考查相似三角形的判定与性质、解直角三角形等知识点,利用三角形相似性质求CF的长是切入点,通过以已知60°角为内角构建直角三角形以表示出两三角形对应边长度比是解题的关键.

练习册系列答案
相关题目
3.将x2+16添加一项,补成一个三项式后恰好是完全平方式,则补上的这个单项式为( )
| A. | 16x | B. | 8x或-8x | C. | 16x或-16x | D. | 8x、-8x或$\frac{1}{64}$x4 |
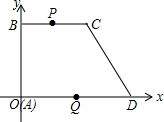 如图.在平面直角坐标系中,梯形ABCD的顶点坐标分别为A(0,0),B(0,8),C(8,8),D(12,0),点P,Q分别从B,D出发以1个单位长度/秒和2个单位长度/秒的速度向C,O出发.设运动时间为t秒(点P到达C点或点Q到达O点,两点均停止运动).
如图.在平面直角坐标系中,梯形ABCD的顶点坐标分别为A(0,0),B(0,8),C(8,8),D(12,0),点P,Q分别从B,D出发以1个单位长度/秒和2个单位长度/秒的速度向C,O出发.设运动时间为t秒(点P到达C点或点Q到达O点,两点均停止运动).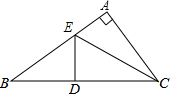 如图,在△ABC中,∠A=90°,DE垂直平分BC,求证:BE2-AE2=AC2.
如图,在△ABC中,∠A=90°,DE垂直平分BC,求证:BE2-AE2=AC2.
 如图,△ABC是等边三角形,点D、E分别是BC、CA延长线上的点,且CD=AE,DA的延长线交BE于点F.
如图,△ABC是等边三角形,点D、E分别是BC、CA延长线上的点,且CD=AE,DA的延长线交BE于点F.