题目内容
18.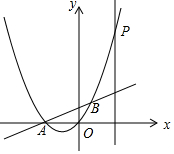 如图,抛物线y=x2+2x与直线y=$\frac{1}{2}$x+1交于A、B两点,与直线x=2交于点P,将抛物线沿着射线AB平移$\frac{3}{2}\sqrt{5}$个单位.
如图,抛物线y=x2+2x与直线y=$\frac{1}{2}$x+1交于A、B两点,与直线x=2交于点P,将抛物线沿着射线AB平移$\frac{3}{2}\sqrt{5}$个单位.(1)平移后的抛物线顶点坐标为(2,$\frac{1}{2}$);
(2)在整个平移过程中,点P经过的路程为$\frac{61}{8}$.
分析 (1)由题意,抛物线沿着射线AB平移$\frac{3}{2}\sqrt{5}$个单位时,点A向右平移3个单位,向上平移$\frac{3}{2}$个单位,根据平移的性质,可得平移后的顶点坐标.
(2)设抛物线向右平移a个单位,则向上平移$\frac{1}{2}$a个单位,抛物线的解析式为y=(x+1-a)2-1+$\frac{a}{2}$,令x=2,y=(3-a)2-1+$\frac{1}{2}$a,可得y=a2-$\frac{11}{2}$a+8,推出y=(a-$\frac{11}{4}$)2+$\frac{7}{16}$,由0≤a≤3,推出y的最大值为8,最小值为$\frac{7}{16}$,又a=3时,y=$\frac{1}{2}$,根据点P的纵坐标的变化情形,即可解决问题.
解答 解:(1)由题意,抛物线沿着射线AB平移$\frac{3}{2}\sqrt{5}$个单位时,点A向右平移3个单位,向上平移$\frac{3}{2}$个单位,
∵抛物线y=x2+2x的顶点坐标为(-1,-1),
∴平移后抛物线的顶点坐标为(2,$\frac{1}{2}$),
故答案为(2,$\frac{1}{2}$).
(2)设抛物线向右平移a个单位,则向上平移$\frac{1}{2}$a个单位,
抛物线的解析式为y=(x+1-a)2-1+$\frac{a}{2}$,
令x=2,y=(3-a)2-1+$\frac{1}{2}$a,
∴y=a2-$\frac{11}{2}$a+8,
∴y=(a-$\frac{11}{4}$)2+$\frac{7}{16}$,
∵0≤a≤3,
∴y的最大值为8,最小值为$\frac{7}{16}$,
∵a=3时,y=$\frac{1}{2}$,
∴点P的经过的路程为8-$\frac{1}{2}$+2($\frac{1}{2}$-$\frac{7}{16}$)=$\frac{61}{8}$,
故答案为$\frac{61}{8}$.
点评 本题考查二次函数图象与几何变换,一次函数图象上点的特征等知识,解题的关键是灵活运用平移的性质解决问题,学会利用参数,构建二次函数解决问题,属于中考压轴题.

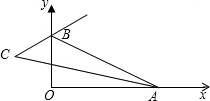 如图,在平面直角坐标系中,A、B分别为x轴、y轴正半轴上两动点,∠BAO的平分线与∠OBA的外角平分线所在直线交于点C,则∠C的度数随A、B运动的变化情况正确的是( )
如图,在平面直角坐标系中,A、B分别为x轴、y轴正半轴上两动点,∠BAO的平分线与∠OBA的外角平分线所在直线交于点C,则∠C的度数随A、B运动的变化情况正确的是( )| A. | 点B不动,在点A向右运动的过程中,∠C的度数逐渐减小 | |
| B. | 点A不动,在点B向上运动的过程中,∠C的度数逐渐减小 | |
| C. | 在点A向左运动,点B向下运动的过程中,∠C的度数逐渐增大 | |
| D. | 在点A、B运动的过程中,∠C的度数不变 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,已知OP平分∠MON,PE⊥OM,垂足为点E,PF⊥ON,垂足为点F,OA=OB,则图中有3对全等三角形.
如图,已知OP平分∠MON,PE⊥OM,垂足为点E,PF⊥ON,垂足为点F,OA=OB,则图中有3对全等三角形.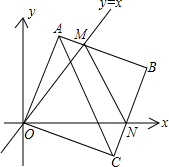 如图①,在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,O为坐标原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.
如图①,在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,O为坐标原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.