题目内容
15.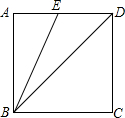 如图,已知正方形ABCD的边长为2,连接BD,BE平分∠ABD并交AD于点E,则DE的长是( )
如图,已知正方形ABCD的边长为2,连接BD,BE平分∠ABD并交AD于点E,则DE的长是( )| A. | 2 | B. | 2$\sqrt{2}$-2 | C. | 4-2$\sqrt{2}$ | D. | 4 |
分析 过点E作EF⊥BD于点F,由角平分线的性质可得AE=EF,易求BD的长,易证△DFE是等腰直角三角形,所以利用勾股定理即可求出DE的长.
解答 解:过点E作EF⊥BD于点F,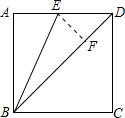
∵四边形ABCD是正方形,
∴∠A=90°,AB=AD=BC=DC=2,∠EDF=45°,
∴△DFE是等腰直角三角形,
∵BE平分∠ABD并交AD于点E,
∴AE=EF,
∵BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=2$\sqrt{2}$,
∴DF=BD-BF=BD-AB=2$\sqrt{2}$-2,
∴EF=DF=2$\sqrt{2}$-2,
∴DE=$\sqrt{2}$DF=4-2$\sqrt{2}$,
故选C.
点评 本题考查了角平分线性质和正方形性质,勾股定理的应用,注意:角平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目
6. 如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
(1)求∠CAD的度数;
(2)若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.
 如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.(1)求∠CAD的度数;
(2)若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.
3.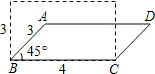 如图,矩形的长和宽分别是4和3,当矩形被“压扁”成内角为45°的平行四边形时,面积大约变成了原来的( )
如图,矩形的长和宽分别是4和3,当矩形被“压扁”成内角为45°的平行四边形时,面积大约变成了原来的( )
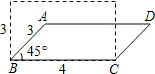 如图,矩形的长和宽分别是4和3,当矩形被“压扁”成内角为45°的平行四边形时,面积大约变成了原来的( )
如图,矩形的长和宽分别是4和3,当矩形被“压扁”成内角为45°的平行四边形时,面积大约变成了原来的( )| A. | 50% | B. | 60% | C. | 70% | D. | 80% |
10. 如图,直线AB、CD、EF交于点O,则图中与∠AOC互为对顶角的是( )
如图,直线AB、CD、EF交于点O,则图中与∠AOC互为对顶角的是( )
 如图,直线AB、CD、EF交于点O,则图中与∠AOC互为对顶角的是( )
如图,直线AB、CD、EF交于点O,则图中与∠AOC互为对顶角的是( )| A. | ∠BOE | B. | ∠BOD | C. | ∠DOE | D. | ∠BOC |
7.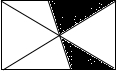 小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是( )
小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是( )
 小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是( )
小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
5.已知点P(x,y)的坐标满足|x|=3,$\sqrt{y}$=2,且xy<0,则点P的坐标是( )
| A. | (3,-2) | B. | (-3,2) | C. | (3,-4) | D. | (-3,4) |
 如图,在?ABCD中,小平行四边形沿对角线AC平移两次就到了图中的位置(阴影部分),若小平行四边形的面积是2,则?ABCD面积是18.
如图,在?ABCD中,小平行四边形沿对角线AC平移两次就到了图中的位置(阴影部分),若小平行四边形的面积是2,则?ABCD面积是18.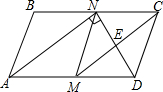 如图,在平行四边形ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点E.
如图,在平行四边形ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点E.