题目内容
4.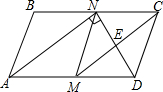 如图,在平行四边形ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点E.
如图,在平行四边形ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点E.(1)求证:△ABN≌△CDM;
(2)猜想四边形CDMN的形状,并说明理由.
分析 (1)直接利用平行四边形的性质得出AB=DC,BC=AD,∠B=∠ADC,再利用M,N分别是AD,BC的中点,得出BN=DM,进而利用全等三角形的判定方法得出答案;
(2)利用直角三角形形的性质结合菱形的判定方法得出答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,BC=AD,∠B=∠ADC,
∵M,N分别是AD,BC的中点,
∴BN=DM,
在△ABN和△CDM中
$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠CDM}\\{BN=MD}\end{array}\right.$,
∴△ABN≌△CDM(SAS);
(2)解:四边形CDMN是菱形,
理由:∵M是AD的中点,∠AND=90°,
∴NM=AM=MD,
∵BN=NC=AM=DM,
∴NC=MN=DM,
∵NC$\stackrel{∥}{=}$DM,
∴四边形CDMN是平行四边形,
又∵MN=DM,
∴四边形CDMN是菱形.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质、菱形的判定等知识,正确应用直角三角形的性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.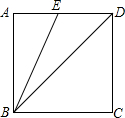 如图,已知正方形ABCD的边长为2,连接BD,BE平分∠ABD并交AD于点E,则DE的长是( )
如图,已知正方形ABCD的边长为2,连接BD,BE平分∠ABD并交AD于点E,则DE的长是( )
 如图,已知正方形ABCD的边长为2,连接BD,BE平分∠ABD并交AD于点E,则DE的长是( )
如图,已知正方形ABCD的边长为2,连接BD,BE平分∠ABD并交AD于点E,则DE的长是( )| A. | 2 | B. | 2$\sqrt{2}$-2 | C. | 4-2$\sqrt{2}$ | D. | 4 |
 (1)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DAO.
(1)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DAO. 如图,直线l上有A、B两点,AB=24cm,点O是线段AB上的一点,OA=2OB.
如图,直线l上有A、B两点,AB=24cm,点O是线段AB上的一点,OA=2OB.