题目内容
7．
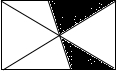小明把如图所示的矩形纸板挂在墙上，玩飞镖游戏（每次飞镖均落在纸板上），则飞镖落在阴影区域的概率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{4}$ |
分析 先根据矩形的性质求出矩形对角线所分的四个三角形面积相等，再求出S1=S2即可．
解答 
解：根据矩形的性质易证矩形的对角线把矩形分成的四个三角形均为同底等高的三角形，故其面积相等，
根据平行线的性质易证S1=S2，故阴影部分的面积占一份，
则飞镖落在阴影区域的概率是$\frac{1}{4}$；
故选D．
点评 此题主要考查了几何概率问题，用到的知识点为：概率=相应的面积与总面积之比．
练习册系列答案
相关题目
17．石市交通系统利用春节植树的大好时机，积极做好公路绿化新植、补值和抚育工作，为省会勾画“满眼是绿”“车在画中游”的美景，现计划在某段公路栽树，要求每两棵树的间隔相等，且公路两端各栽一棵，若每隔4米栽一棵，则树苗缺200棵，若每隔5米栽一棵，则树苗正好用完，求原树苗多少棵？设原有树苗x棵，则根据题意列出的正确方程是（ ）
| A． | 4（x+200-1）=5（x-1） | B． | 4（x+200）=5（x-1） | C． | 4（x+200-1）=5x | D． | 4（x+200）=5x |
18．下列运算中，正确的是（ ）
| A． | a3•a4=a12 | B． | （2a）2•（-a）3=2a6 | C． | -（-a）2•（-a）3=a6 | D． | -（-a）2•a4=-a6 |
15．
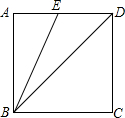如图，已知正方形ABCD的边长为2，连接BD，BE平分∠ABD并交AD于点E，则DE的长是（ ）
如图，已知正方形ABCD的边长为2，连接BD，BE平分∠ABD并交AD于点E，则DE的长是（ ）| A． | 2 | B． | 2$\sqrt{2}$-2 | C． | 4-2$\sqrt{2}$ | D． | 4 |
如图是由相交线按一定规律平移所构成的一系列图形，其中①有2组平行线，②有6组平行线，③有12组平行线，…以此类推，⑥有42组平行线．
（1）如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH，求证：∠DHO=∠DAO．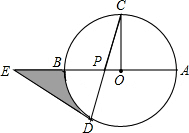
如图，⊙O的半径OC与直径AB垂直，点P在OB上，CP的延长线交⊙O于点D，在OB的延长线上取点E，使ED=EP．