题目内容
3.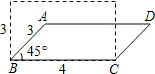 如图,矩形的长和宽分别是4和3,当矩形被“压扁”成内角为45°的平行四边形时,面积大约变成了原来的( )
如图,矩形的长和宽分别是4和3,当矩形被“压扁”成内角为45°的平行四边形时,面积大约变成了原来的( )| A. | 50% | B. | 60% | C. | 70% | D. | 80% |
分析 过A作AQ⊥BC于Q,通过解直角三角形求出AQ,求出平行四边形的面积和矩形的面积,即可求出答案.
解答 解:过A作AQ⊥BC于Q,如图所示:
∵sin∠ABQ=$\frac{AQ}{AB}$,∠ABQ=45°,AB=3,
∴AQ=$\frac{3\sqrt{2}}{2}$,
∴S平行四边形BCFE=BC×AQ=4×$\frac{3\sqrt{2}}{2}$=6$\sqrt{2}$,
∵S矩形ABCD=BC×AB=4×3=12,
∴$\frac{6\sqrt{2}}{12}$=$\frac{\sqrt{2}}{2}$≈0.7=70%,
故选:C.
点评 本题考查了平行四边形的性质,矩形的性质,解直角三角形等知识点,关键是求出矩形和平行四边形的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列运算中,正确的是( )
| A. | a3•a4=a12 | B. | (2a)2•(-a)3=2a6 | C. | -(-a)2•(-a)3=a6 | D. | -(-a)2•a4=-a6 |
8.2013年12月2日凌晨,我国长征系列火箭中运载能力最强的“大力士”--长三乙增强型火箭将3780公斤重的“嫦娥三号”精准地送入远地点380000公里的地月转移轨道.380000用科学记数法表示为( )
| A. | 3.8×104 | B. | 3.8×105 | C. | 0.38×105 | D. | 0.38×104 |
15.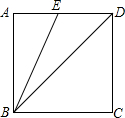 如图,已知正方形ABCD的边长为2,连接BD,BE平分∠ABD并交AD于点E,则DE的长是( )
如图,已知正方形ABCD的边长为2,连接BD,BE平分∠ABD并交AD于点E,则DE的长是( )
 如图,已知正方形ABCD的边长为2,连接BD,BE平分∠ABD并交AD于点E,则DE的长是( )
如图,已知正方形ABCD的边长为2,连接BD,BE平分∠ABD并交AD于点E,则DE的长是( )| A. | 2 | B. | 2$\sqrt{2}$-2 | C. | 4-2$\sqrt{2}$ | D. | 4 |
 (1)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DAO.
(1)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DAO.