题目内容
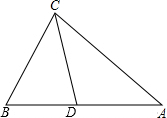 如图,已知:在△ABC中,CD是∠ACB的平分线.求证:BC:AC=BD:AD.
如图,已知:在△ABC中,CD是∠ACB的平分线.求证:BC:AC=BD:AD.考点:角平分线的性质,相似三角形的判定与性质
专题:证明题
分析:过点B作BE∥AC交CD的延长线于E,根据两直线平行,内错角相等可得∠E=∠ACD,根据角平分线的定义可得∠BCD=∠ACD,从而得到∠BCD=∠E,根据等角对等边可得BC=BE,再求出△BED和△ACD相似,然后根据相似三角形对应边成比例列式整理即可得解.
解答: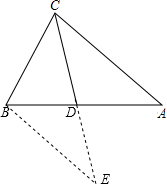 证明:如图,过点B作BE∥AC交CD的延长线于E,
证明:如图,过点B作BE∥AC交CD的延长线于E,
∴∠E=∠ACD,
∵CD是∠ACB的平分线,
∴∠BCD=∠ACD,
∴∠BCD=∠E,
∴BC=BE,
由BE∥AC得,△BED∽△ACD,
∴BE:AC=BD:AD,
∴BC:AC=BD:AD.
 证明:如图,过点B作BE∥AC交CD的延长线于E,
证明:如图,过点B作BE∥AC交CD的延长线于E,∴∠E=∠ACD,
∵CD是∠ACB的平分线,
∴∠BCD=∠ACD,
∴∠BCD=∠E,
∴BC=BE,
由BE∥AC得,△BED∽△ACD,
∴BE:AC=BD:AD,
∴BC:AC=BD:AD.
点评:本题考查了角平分线性质的证明,相似三角形的判定与性质,作辅助线构造出等腰三角形和相似三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
 如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABE、等边△ACD、等边△BCF.
如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABE、等边△ACD、等边△BCF.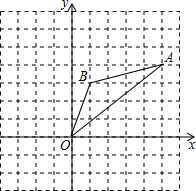 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1. 如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB:AD=2:3,那么tan∠EFC值是
如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB:AD=2:3,那么tan∠EFC值是