题目内容
 如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB:AD=2:3,那么tan∠EFC值是
如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB:AD=2:3,那么tan∠EFC值是考点:翻折变换(折叠问题)
专题:几何图形问题
分析:根据AB:AD=2:3,以及折叠的性质表示出三角形ABF的各边长,然后利用等角变换得出∠BAF=∠CFE,继而可得出答案.
解答:解:∵AB:AD=2:3,
∴在Rt△ABF中,设AB=2x,AF=AD=BC=3x,
则BF=
=
x,
又∵∠EFC+∠AFB=90°,∠AFB+∠BAF=90°,
∴∠BAF=∠CFE,
故tan∠EFC=tan∠BAF=
=
=
.
故答案为:
.
∴在Rt△ABF中,设AB=2x,AF=AD=BC=3x,
则BF=
| AF2-AB2 |
| 5 |
又∵∠EFC+∠AFB=90°,∠AFB+∠BAF=90°,
∴∠BAF=∠CFE,
故tan∠EFC=tan∠BAF=
| BF |
| AB |
| ||
| 2x |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了翻折变换及锐角三角函数的定义,解答本题的关键是解直角三角形ABF,另外要得出重要的一点是∠BAF=∠CFE.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
在实数0,
,
,
,π,
中,无理数一共有( )
| 2 |
| 5 |
| 7 |
| 3 | 4 |
| 25 |
| A、1个 | B、2个 | C、3个 | D、4个 |
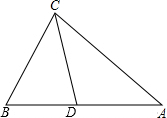 如图,已知:在△ABC中,CD是∠ACB的平分线.求证:BC:AC=BD:AD.
如图,已知:在△ABC中,CD是∠ACB的平分线.求证:BC:AC=BD:AD.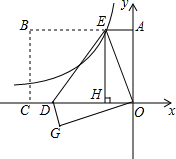 如图,在直角坐标系中,矩形OABC的顶点C在x轴的负半轴上,点A在y轴正半轴上,矩形OABC的面积为
如图,在直角坐标系中,矩形OABC的顶点C在x轴的负半轴上,点A在y轴正半轴上,矩形OABC的面积为