题目内容
11.善于学习的小敏查资料知道:对应角相等,对应边成比例的两个梯形,叫做相似梯形.他想到“平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似”,提出如下两个问题,你能帮助解决吗?【问题一】平行于梯形底边的直线截两腰所得的小梯形和原梯形是否相似?
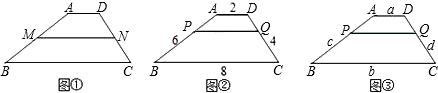
(1)从特殊情形入手探究.假设梯形ABCD中,AD∥BC,AB=6,BC=8,CD=4,AD=2,MN是中位线(如图①).根据相似梯形的定义,请你说明梯形AMND与梯形ABCD是否相似?
(2)一般结论:平行于梯形底边的直线截两腰所得的梯形与原梯形不相似(填“相似”或“不相似”或“相似性无法确定”,不要求证明)
【问题二】平行于梯形底边的直线截两腰所得的两个小梯形和原梯形是否相似?
(1)从特殊平行线入手探究,梯形的中位线截两腰所得的两个小梯形不相似(填“相似”或“不相似”或“相似性无法确定”,不要求证明)
(2)从特殊梯形入手探究.同上假设,梯形ABCD中,AD∥BC,AB=6,BC=8,CD=4,AD=2,你能找到与梯形底边平行的直线PQ(点PQ在梯形的两腰上,如图②),使得梯形APQD与梯形PBCQ相似吗?请根据相似梯形的定义说明理由.
(3)一般结论:对于任意梯形(如图③),一定存在(填“存在”或“不存在”)平行于梯形底边的直线PQ,使截得的两个小梯形相似?若存在,则确定这条平行线位置的条件是$\frac{AP}{PB}$=$\frac{\sqrt{ab}}{b}$(设AD=a,BC=b,AB=c,CD=d.用含a、b的式子表示 ).
分析 问题一:(1)根据两个梯形相似,因而两个梯形的对应腰的相等,对应底的比相等;这个图形中判定相似要同时满足这几个条件.反之,若相似则两个梯形的对应腰的相等,对应底的比相等判断即可;
(2)根据两个梯形的对应腰的相等,对应底的比相等判断即可;
问题二:(1)根据两个梯形的对应腰的相等,对应底的比相等判断即可;
(2)假设梯形APQD与梯形PBCQ相似,于是得到$\frac{AD}{PQ}$=$\frac{PQ}{BC}$,即$\frac{2}{PQ}$=$\frac{PQ}{8}$得到PQ=4.由于$\frac{AP}{PB}$=$\frac{AD}{PQ}$=$\frac{2}{4}$=$\frac{1}{2}$.得到AP=2,PB=4,根据$\frac{DQ}{QC}=\frac{1}{2}$,CD=4,得到$DQ=\frac{4}{3},QC=\frac{8}{3}$,于是得到$\frac{AD}{PQ}=\frac{PQ}{BC}=\frac{PA}{PB}=\frac{DQ}{QC}$,由于两梯形中对应角相等,于是得到结论;
(3)如果梯形APQD∽梯形PBCQ,得到$\frac{AD}{PQ}$=$\frac{PQ}{BC}$,$\frac{AP}{PB}$=$\frac{AD}{PQ}$,代入即可得到结果.
解答 解:问题一:(1)两个梯形的腰相等,
即腰的比是1:2,而上底的比是1:1,
因而这两个梯形一定不相似;
(2)不相似,
故答案为:不相似;
问题二:(1)不相似;
故答案为:不相似;
(2)梯形APQD与梯形PBCQ相似,
∴$\frac{AD}{PQ}$=$\frac{PQ}{BC}$,即$\frac{2}{PQ}$=$\frac{PQ}{8}$
解得:PQ=4.
∵$\frac{AP}{PB}$=$\frac{AD}{PQ}$=$\frac{2}{4}$=$\frac{1}{2}$.
又∵AP+PB=6,
∴AP=2,PB=4,
∵$\frac{DQ}{QC}=\frac{1}{2}$,CD=4,
∴$DQ=\frac{4}{3},QC=\frac{8}{3}$,
∴$\frac{AD}{PQ}=\frac{PQ}{BC}=\frac{PA}{PB}=\frac{DQ}{QC}$,
又∵两梯形中对应角相等,
∴梯形APQD相似于梯形PBCQ;
(3)如果梯形APQD∽梯形PBCQ,
则$\frac{AD}{PQ}$=$\frac{PQ}{BC}$,$\frac{AP}{PB}$=$\frac{AD}{PQ}$,
∵AD=a,BC=b,
∴PQ=$\sqrt{AD•BC}$=$\sqrt{ab}$,
∴$\frac{AP}{PB}$=$\frac{a}{\sqrt{ab}}$=$\frac{\sqrt{ab}}{b}$.
点评 本题考查了等腰梯形的性质,梯形相似的判定和性质,勾股定理,相似梯形的性质是:对应角相等,对应边的比相等,反之,相似图形的判定方法是对应角相等,对应边的比相等,熟练掌握相似梯形的判定和性质定理是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,直线l1∥l2,则∠a的度数是( )
如图,直线l1∥l2,则∠a的度数是( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
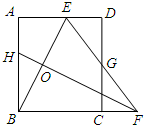 如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是( )
如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是( ) 如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E.求证:四边形OCED是菱形.
如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E.求证:四边形OCED是菱形. 已知菱形ABCD周长为8,一组邻角之比为1:2,求菱形对角线AC、BD的长和菱形的面积.
已知菱形ABCD周长为8,一组邻角之比为1:2,求菱形对角线AC、BD的长和菱形的面积.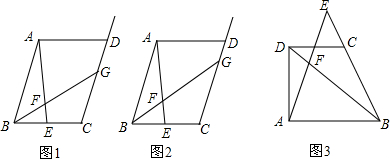
 如图,已知直线的函数表达式为y=-$\frac{4}{3}$x+8,且l与x轴,y轴分别交于A,B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.
如图,已知直线的函数表达式为y=-$\frac{4}{3}$x+8,且l与x轴,y轴分别交于A,B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒. 已知:如图,AB=DC,∠A=∠D,∠1=∠2
已知:如图,AB=DC,∠A=∠D,∠1=∠2