题目内容
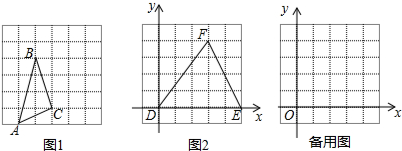
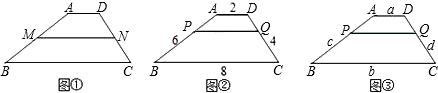
1.正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.(1)如图1中,点A、B、C均在格点上.求出△ABC的面积;
(2)在图2正方形网格(每个小正方形边长为1)中以D为坐标原点建立如图所示的直角坐标系,若格点△DEF满足DE=DF=5,EF=2$\sqrt{5}$,点E在坐标轴上,请画出符合题意的图形;(注意两解哦!)
(3)求出(2)中直线EF的一次函数表达式.
分析 (1)根据S△ABM=S矩形APNM-S△ABM-S△APC-S△BNC即可求解;
(2)图(2)中的△DEF和它关于y轴的对称三角形符合条件;
(3)利用待定系数法即可求得函数的解析式.
解答 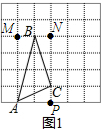 解:(1)S矩形APNM=2×4=8,
解:(1)S矩形APNM=2×4=8,
S△ABM=$\frac{1}{2}$×4×1=2,S△APC=$\frac{1}{2}$×2×1=1,S△BNC=$\frac{1}{2}$×1×3=$\frac{3}{2}$,
则S△ABC=8-2-1-$\frac{3}{2}$=$\frac{7}{2}$;
(2)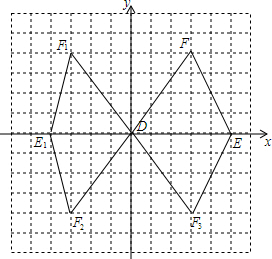
△DEF和三角形DE1F1,△DEF3,△DE1F2都是所求的三角形;
(3)△DEF中,E的坐标是(5,0),F的坐标是(3,4),设直线EF的解析式是y=kx+b
则$\left\{\begin{array}{l}{5k+b=0}\\{3k+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=10}\end{array}\right.$,
则直线EF的解析式是y=-2x+10,
同理E1F1的解析式是y=2x+10,
E1F2的解析式是y=-2x-10,
EF3的解析式是y=2x-10.
总之,EF的解析式是y=-2x+10或y=2x+10或y=-2x-10或y=2x-10.
点评 本题考查了待定系数法求函数解析式,注意到△DEF的三边的长度确定,则三角形的形状、大小都确定,则可以通过图(2)中的三角形对折进行变换得到是关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
12.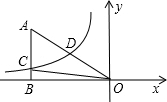 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-4,6),则△AOC的面积为( )
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-4,6),则△AOC的面积为( )
 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-4,6),则△AOC的面积为( )
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-4,6),则△AOC的面积为( )| A. | 4 | B. | 6 | C. | 9 | D. | 12 |
6.∑表示数学中的求和符号,主要用于求多个数的和,∑下面的小字,i=1表示从1开始求和;上面的小字,如n表示求和到n为止.即$\sum_{i=1}^{n}$xi=x1+x2+x3+…+xn.则$\sum_{i=1}^{n}$(i2-1)表示( )
| A. | n2-1 | B. | 12+22+32+…+n2-(1+2+3+…+n ) | ||
| C. | 12+22+32+…+n2-n | D. | 12+22+32+…+i2-i |
 如图,在△ABC中,AB=4,AC=3,BC=5,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为6.
如图,在△ABC中,AB=4,AC=3,BC=5,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为6.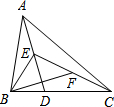 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为18cm2,则△BEF的面积为( )
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为18cm2,则△BEF的面积为( ) 如图,如图,在△ABC中,DE∥BC,若$\frac{AD}{AB}=\frac{1}{3}$,已知DE=3cm,
如图,如图,在△ABC中,DE∥BC,若$\frac{AD}{AB}=\frac{1}{3}$,已知DE=3cm,