题目内容
12.用配方法解方程x2-6x+2=0,原方程可变形为( )| A. | (x-3)2=11 | B. | (x-3)2=7 | C. | (x+3)2=7 | D. | (x-3)2=2 |
分析 利用完全公式可把原方程表示为(x-3)2=7.
解答 解:x2-6x=-2,
x2-6x+9=-2+9
(x-3)2=7.
故选B.
点评 本题考查了解一元二次方程-配方法:将一元二次方程配成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为-5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为$\frac{1}{3}$BC的点N,则该数轴的原点为( )
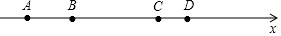
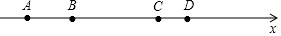
| A. | 点E | B. | 点F | C. | 点M | D. | 点N |
3.若a<0,则下列不等式不成立的是( )
| A. | a+2<a+3 | B. | 2a<3a | C. | 2-a<3-a | D. | $\frac{a}{2}$<$\frac{a}{3}$ |
7.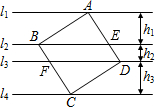 如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3.若h1=2,h2=1,则正方形ABCD的面积为( )
如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3.若h1=2,h2=1,则正方形ABCD的面积为( )
 如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3.若h1=2,h2=1,则正方形ABCD的面积为( )
如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3.若h1=2,h2=1,则正方形ABCD的面积为( )| A. | 9 | B. | 10 | C. | 13 | D. | 25 |
4.下列根式中,不是最简二次根式的是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{2}$ | C. | $\sqrt{12}$ | D. | $\sqrt{22}$ |
2.在下列正多边形瓷砖中,如果仅用一种正多变形瓷砖铺地面,那么不能将地面密铺的是( )
| A. | 正三角形 | B. | 正四边形 | C. | 正五边形 | D. | 正六边形 |
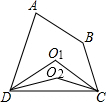 如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是175°.
如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是175°. 如图是一个底面为正三角形的直三棱柱,则这个几何体的主视图是( )
如图是一个底面为正三角形的直三棱柱,则这个几何体的主视图是( )


