题目内容
9. 如图,平行四边形ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=1,则AB的长是1.
如图,平行四边形ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=1,则AB的长是1.
分析 首先证明四边形ABDE是平行四边形,AB=DE=CD,即D是CE的中点,在直角△CEF中求得到CE的长,则求得CD,进而根据AB=CD求解.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,
即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,
∴CE=2CF=2,
∴AB=1;
故答案为:1.
点评 本题考查了平行四边形的判定与性质,以及三角函数的应用,正确理解D是CE的中点是关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
19.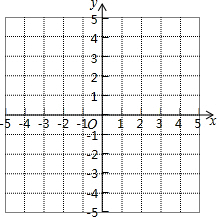 小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y=|x-1|的自变量x的取值范围是任意实数;
(2)列表,找出y与x的几组对应值.
其中,b=2;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质:函数的最小值为0(答案不唯一).
 小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:(1)函数y=|x-1|的自变量x的取值范围是任意实数;
(2)列表,找出y与x的几组对应值.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | b | 1 | 0 | 1 | 2 | … |
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质:函数的最小值为0(答案不唯一).
4.下列根式中,不是最简二次根式的是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{2}$ | C. | $\sqrt{12}$ | D. | $\sqrt{22}$ |
14.点A(-2,5)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,则k的值是( )
| A. | 10 | B. | 5 | C. | -5 | D. | -10 |
19.式子$\frac{1}{\sqrt{3-a}}$有意义,则a的取值范围是( )
| A. | a<3 | B. | a≤3 | C. | a>3 | D. | a≥3 |
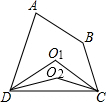 如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是175°.
如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是175°. 如图是一个底面为正三角形的直三棱柱,则这个几何体的主视图是( )
如图是一个底面为正三角形的直三棱柱,则这个几何体的主视图是( )


