题目内容
19. 如图,在△ABC中,AB=AC,AD为△ABC的中线,O为AB上一点,以O为圆心,AO为半径的⊙O与AB交于点F,与BC交于点E.连接AE,AE平分∠BAD.
如图,在△ABC中,AB=AC,AD为△ABC的中线,O为AB上一点,以O为圆心,AO为半径的⊙O与AB交于点F,与BC交于点E.连接AE,AE平分∠BAD.(1)求证:BC与⊙O相切于点E;
(2)若AB=10,BC=16,求⊙O的半径;
(3)若AD与⊙O的交点为△ABC的重心,则$\frac{△ABE的面积}{△ABC的面积}$的值为$\frac{1}{3}$.
分析 (1)利用OA=OE得出∠AEO=∠OAE,再由角平分线得出∠BAE=∠DAE,即得出OE∥AD即可;
(2)先求出BD=8,再用勾股定理求出AD=6,进而用角平分线定理即可得出BE=5,最后用相似三角形的性质得出结论;
(3)先用切割线定理得出DE,进而用勾股定理得出AE,∠BAE=30°,即可得出BE=AE,即可得出结论.
解答 解:(1)如图1,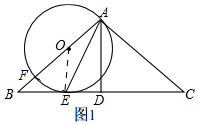 连接OE,
连接OE,
∴OA=OE,
∴∠AEO=∠OAE,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠AEO=∠DAE,
∴OE∥AD,
在△ABC中,AB=AC,AD为△ABC的中线,
∴AD⊥BC,
∴OE⊥BC,
∵点E在⊙O上,
∴BC与⊙O相切于点E;
(2)如图1,在△ABC中,AB=AC,AD为△ABC的中线,
∴AD⊥BC,BD=CD=$\frac{1}{2}$BC=8,
在Rt△ABD中,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=6,
∵AE平分∠BAD,
∴$\frac{AD}{AB}=\frac{DE}{BE}$,
∴$\frac{ED}{BE}=\frac{6}{10}=\frac{3}{5}$,
∴DE=$\frac{3}{5}$BE,
∵BD=BE+DE=8,
∴BE+$\frac{3}{5}$BE=8,
∴BE=5,
由(1)知,OE∥AD,
∴△OBE∽△ABD,
∴$\frac{OE}{AD}=\frac{BE}{BD}$,
∴$\frac{OE}{6}=\frac{5}{8}$,
∴OE=$\frac{15}{4}$,
∴⊙O的半径为$\frac{15}{4}$;
(3)如图2,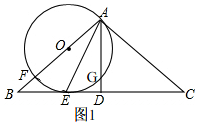 记AD与⊙O的交点为△ABC的重心为G,
记AD与⊙O的交点为△ABC的重心为G,
设DG=x,
∴AD=3x,
∵DE是⊙O的切线,根据切割线定理得,DE2=DG•AD=x•3x=3x2,
∴DE=$\sqrt{3}$x,
在Rt△ADE中,AD=3x,DE=$\sqrt{3}$x,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=2$\sqrt{3}$x,tan∠DAE=$\frac{DE}{AD}$=$\frac{\sqrt{3}x}{3x}$=$\frac{\sqrt{3}}{3}$,
∴∠DAE=30°,
∵AE平分∠BAD,
∴∠BAD=2∠BAE=2∠DAE=60°,
∴∠BAE=30°,
∴∠ABE=90°-∠BAD=90°-2∠ADE=30°=∠BAE,
∴BE=AE=2$\sqrt{3}$x,BC=2BD=2(BE+DE)=2(2$\sqrt{3}$x+$\sqrt{3}$x)=6$\sqrt{3}$x
∴$\frac{△ABE的面积}{△ABC的面积}$=$\frac{\frac{1}{2}BE•AD}{\frac{1}{2}BC•AD}$=$\frac{BE}{BC}$=$\frac{2\sqrt{3}x}{6\sqrt{3}x}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题是圆的综合题,主要考查了切线的判定,等腰三角形的中线,勾股定理,角平分线定理,相似三角形的判定和性质,锐角三角函数等知识点,解答(1)的关键是得出OE∥AD,解答(2)的关键是利用角平分线定理求出BE,解答(3)的关键是求出∠BAE=30°是解本题的关键.

| A. | $\frac{4}{20}-\frac{x}{20}-\frac{x}{12}=1$ | B. | $\frac{4}{20}-\frac{x}{20}+\frac{x}{12}=1$ | C. | $\frac{4}{20}+\frac{x}{20}-\frac{x}{12}=1$ | D. | $\frac{4}{20}+\frac{x}{20}+\frac{x}{12}=1$ |
| A. | 3 | B. | -4 | C. | 4 | D. | 5 |
| A. | a(b-c)=ab-ac | B. | x2-2x+3=(x-1)2+2 | C. | x2-4=(x+2)(x-2) | D. | (x+1)(x+2)=x2+3x+2 |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
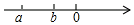 若有理数a,b在数轴上的位置如图所示,则下列判断中错误的是( )
若有理数a,b在数轴上的位置如图所示,则下列判断中错误的是( )| A. | ab>0 | B. | a+b<0 | C. | $\frac{a}{b}$<1 | D. | a-b<0 |