题目内容
7.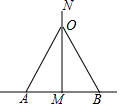 如图,一根长6.5m的电线杆,埋入地下1.5m,需要两根钢丝绳固定,已知固定点距电线杆上端N点1m,电线杆入地点距钢丝绳入地点MA=MB=3m,则两根钢丝绳的长度至少为( )(连接处忽略不计)
如图,一根长6.5m的电线杆,埋入地下1.5m,需要两根钢丝绳固定,已知固定点距电线杆上端N点1m,电线杆入地点距钢丝绳入地点MA=MB=3m,则两根钢丝绳的长度至少为( )(连接处忽略不计)| A. | 14m | B. | 11m | C. | 13m | D. | 10m |
分析 根据题意得出AM,MO的长,再利用勾股定理得出AO,的长即可得出答案.
解答 解:由题意可得:MO=6.5-1.5-1=4(m),AM=3m,
在Rt△AOM中
AO=$\sqrt{O{M}^{2}+A{M}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5(m),
故AO+BO=10m,
则两根钢丝绳的长度至少为10m.
故选:D.
点评 此题主要考查了勾股定理的应用,正确得出AO的长是解题关键.

练习册系列答案
相关题目
2. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.上述结论中正确的是( )
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.上述结论中正确的是( )
 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.上述结论中正确的是( )
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.上述结论中正确的是( )| A. | ②③ | B. | ②④ | C. | ①②③ | D. | ②③④ |
12.已知两个分式:A=$\frac{2}{x-3}$-$\frac{1}{x}$,B=$\frac{x+3}{{x}^{2}-3x}$,其中x≠3且x≠0,则A与B的关系是( )
| A. | 相等 | B. | 互为倒数 | C. | 互为相反数 | D. | 不能确定 |
19.已知a,b,c,d为有理数,现规定一种新的运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,那么当$|\begin{array}{l}{2}&{4}\\{(1-x)}&{5x}\end{array}|$=18时,则x的值是( )
| A. | x=1 | B. | $x=\frac{7}{11}$ | C. | $x=\frac{11}{7}$ | D. | x=-1 |
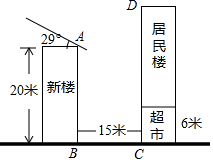 某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)
某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55) 如图,
如图, 在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为7.
在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为7.