题目内容
17.已知反比例函数y=$\frac{k}{x}$(k≠0,k是常数)的图象过点P(-3,5).(1)求此反比例函数的解析式;
(2)判断点Q(-$\frac{15}{2}$,2)是否在图象上;
(3)在函数图象上有两点(a1,b1)和(a2,b2),若a1<a2,试判断b1与b2的大小关系.
分析 (1)直接把点P(-2,3)代入反比例函数y=$\frac{k}{x}$(k≠0,k是常数),求出k的值即可;
(2)把点A(-1,-3)代入反比例函数的解析式进行检验即可;
(3)分两种情况根据反比例函数的性质即可判断.
解答 解:(1)∵将P(-3,5)代入反比例函数y=$\frac{k}{x}$(k≠0,k是常数),得5=$\frac{k}{-3}$,
解得,k=-15.
∴反比例函数表达式为:y=-$\frac{15}{x}$;
(2)反比例函数图象经过点Q.
理由是:∵-$\frac{15}{2}$×2=-15=k,
∴反比例函数图象经过点Q;
(3)①当两点(a1,b1)和(a2,b2)在同一个分支上,由反比例函数y=-$\frac{15}{x}$可知,在每一个象限内,y随x的增大而增大,
∴b1与b2的关系是:b1<b2.
②当两点(a1,b1)和(a2,b2)不在同一个分支上,
∵a1<a2,
∴b1>0,b2<0,
∴b1>b2.
点评 本题考查的是待定系数法求反比例函数的解析式以及反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
5.在同一平面内,下列说法正确的是( )
| A. | 两点之间的距离就是两点间的线段 | |
| B. | 与同一条直线垂直的两条直线也垂直 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 过一点有且只有一条直线与已知直线垂直 |
12.已知某种型号的纸100张的厚度约为1cm,那么这种型号的纸13亿张的厚度约为( )
| A. | 1.3×105km | B. | 1.3×104km | C. | 1.3×103km | D. | 1.3×102km |
 图中的四边形均为矩形.根据图形,写出一个正确的等式:(m+a)(m+b)=m2+am+bm+ab(答案不唯一).
图中的四边形均为矩形.根据图形,写出一个正确的等式:(m+a)(m+b)=m2+am+bm+ab(答案不唯一).
 画一画
画一画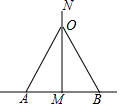 如图,一根长6.5m的电线杆,埋入地下1.5m,需要两根钢丝绳固定,已知固定点距电线杆上端N点1m,电线杆入地点距钢丝绳入地点MA=MB=3m,则两根钢丝绳的长度至少为( )(连接处忽略不计)
如图,一根长6.5m的电线杆,埋入地下1.5m,需要两根钢丝绳固定,已知固定点距电线杆上端N点1m,电线杆入地点距钢丝绳入地点MA=MB=3m,则两根钢丝绳的长度至少为( )(连接处忽略不计)