题目内容
 已知:如图,在△ABC中,点E、F分别是AB、AC上的点,且EF∥BC,BM是线段CF的垂直平分线,垂足为M.N是线段BM上一点,且NC=EF.
已知:如图,在△ABC中,点E、F分别是AB、AC上的点,且EF∥BC,BM是线段CF的垂直平分线,垂足为M.N是线段BM上一点,且NC=EF.(1)若∠BNC=150°,求证:FM=
| 1 |
| 2 |
(2)若BN=BE,求证:∠MNC=3∠MBC.
考点:线段垂直平分线的性质,全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:(1)连接FN,根据线段垂直平分线的性质得出NF=NC,FM=MC,求出∠FNM=∠CNM,∠CNM=30°,推出△CNF是等边三角形,根据等边三角形的性质得出CF=NC即可;
(2)连接BF,求出∠CBM=∠FBM,NF=EF,根据SSS证△FEB≌△FNB,根据全等三角形的性质得出∠EBN=∠NBF,∠BEF=∠BNF,求出∠ABC=3∠MBC,∠AEF=∠FNM,推出∠MNC=∠AEF,∠AEF=∠ABC,即可得出答案.
(2)连接BF,求出∠CBM=∠FBM,NF=EF,根据SSS证△FEB≌△FNB,根据全等三角形的性质得出∠EBN=∠NBF,∠BEF=∠BNF,求出∠ABC=3∠MBC,∠AEF=∠FNM,推出∠MNC=∠AEF,∠AEF=∠ABC,即可得出答案.
解答:证明:(1)连接FN,
∵BM是线段CF的垂直平分线,
∴NF=NC,FM=MC,
∴∠FNM=∠CNM,
∵∠BNC=150°,
∴∠CNM=30°,
∴∠CNF=60°,
∴△CNF是等边三角形,
∴CF=NC,
∵FM=MC,EF=NC,
∴FM=
EF;
(2)连接BF,
∵BM是线段CF的垂直平分线,
∴∠CBM=∠FBM,
∵NC=NF,NC=EF,
∴NF=EF,
在△FEB和△FNB中
∴△FEB≌△FNB,
∴∠EBN=∠NBF,∠BEF=∠BNF,
∵∠CBM=∠FBM,∠BEF+∠AEF=∠BNF+∠FNM=180°,
∴∠ABC=3∠MBC,∠AEF=∠FNM,
∵∠FNM=∠MNC,
∴∠MNC=∠AEF,
∵EF∥BC,
∴∠AEF=∠ABC,
∵∠ABC=3∠MBC,∠MNC=∠AEF,
∴∠MNC=3∠MBC.

∵BM是线段CF的垂直平分线,
∴NF=NC,FM=MC,
∴∠FNM=∠CNM,
∵∠BNC=150°,
∴∠CNM=30°,
∴∠CNF=60°,
∴△CNF是等边三角形,
∴CF=NC,
∵FM=MC,EF=NC,
∴FM=
| 1 |
| 2 |
(2)连接BF,
∵BM是线段CF的垂直平分线,
∴∠CBM=∠FBM,
∵NC=NF,NC=EF,
∴NF=EF,
在△FEB和△FNB中
|
∴△FEB≌△FNB,
∴∠EBN=∠NBF,∠BEF=∠BNF,
∵∠CBM=∠FBM,∠BEF+∠AEF=∠BNF+∠FNM=180°,
∴∠ABC=3∠MBC,∠AEF=∠FNM,
∵∠FNM=∠MNC,
∴∠MNC=∠AEF,
∵EF∥BC,
∴∠AEF=∠ABC,
∵∠ABC=3∠MBC,∠MNC=∠AEF,
∴∠MNC=3∠MBC.
点评:本题考查了线段垂直平分线性质,全等三角形的性质和判定,三角形的外角性质,等腰三角形的性质的应用,能综合性运用性质进行推理是解此题的关键,综合性比较强,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下面的说法中,正确的个数有( )
①柱体的两个底面一样大 ②圆柱、圆锥的底面都是圆 ③棱柱的底面是四边形
④棱柱的侧面一定是长方形(包括正方形) ⑤长方体一定是柱体 ⑥长方体的面不可能是正方形.
①柱体的两个底面一样大 ②圆柱、圆锥的底面都是圆 ③棱柱的底面是四边形
④棱柱的侧面一定是长方形(包括正方形) ⑤长方体一定是柱体 ⑥长方体的面不可能是正方形.
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图所示,轮船在A处观测到北偏东45°方向上有个灯塔B,轮船在正东方向20海里1.5小时后到达C处,又观测到灯塔B在北偏东30°方向上,则此时轮船与灯塔B相距海里.(结果保留根号)
如图所示,轮船在A处观测到北偏东45°方向上有个灯塔B,轮船在正东方向20海里1.5小时后到达C处,又观测到灯塔B在北偏东30°方向上,则此时轮船与灯塔B相距海里.(结果保留根号) 如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.求证:MN⊥BD.
如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.求证:MN⊥BD.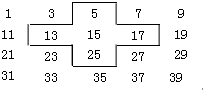 将连续的奇数1,3,5,7,9…排成如下的数表:
将连续的奇数1,3,5,7,9…排成如下的数表: