题目内容
解方程:x(x+1)(x+2)(x+3)+1=0.
考点:换元法解一元二次方程
专题:
分析:先设y=x2+3x,则原方程变形为y2+2y+1=0,运用因式分解法解得y1=y2=-1,再把y=-1代入y=x2+3x得到关于x的一元二次方程,然后解一元二次方程,最后确定原方程的解.
解答:解:整理,得(x2+3x)2+2(x2+3x)+1=0
设y=x2+3x,
原方程变形为y2+2y+1=0,
(y+1)2=0,
解得y1=y2=-1,
∴x2+3x+1=0,
解得x=
=
∴x1=
,x2=
,
所以原方程的解为x1=
,x2=
.
设y=x2+3x,
原方程变形为y2+2y+1=0,
(y+1)2=0,
解得y1=y2=-1,
∴x2+3x+1=0,
解得x=
-3±
| ||
| 2×1 |
-3±
| ||
| 2 |
∴x1=
-3+
| ||
| 2 |
-3-
| ||
| 2 |
所以原方程的解为x1=
-3+
| ||
| 2 |
-3-
| ||
| 2 |
点评:本题考查了换元法解一元二次方程:我们常用的是整体换元法,是在已知或者未知中,某个代数式几次出现,而用一个字母来代替它从而简化问题,当然有时候要通过变形才能发现.把一些形式复杂的方程通过换元的方法变成一元二次方程,从而达到降次的目的.

练习册系列答案
相关题目

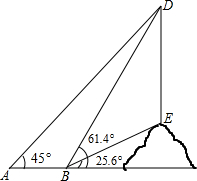 如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米?(结果精确到个位)(参考数据:sin25.6°≈0.4,cos25.6°≈0.9,tan25.6°≈0.5,sin61.4°≈0.9,cos61.4°≈0.5,tan61.4°≈1.8)
如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米?(结果精确到个位)(参考数据:sin25.6°≈0.4,cos25.6°≈0.9,tan25.6°≈0.5,sin61.4°≈0.9,cos61.4°≈0.5,tan61.4°≈1.8)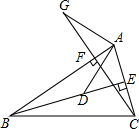 如图,BE,CF分别是△ABC的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AG,AD.求证:
如图,BE,CF分别是△ABC的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AG,AD.求证: