题目内容
2.若|x+y-5|+(x-y+1)2=0,则x2-y2=-5.分析 利用非负数的性质求出x+y与x-y的值,原式利用平方差公式分解后代入计算即可求出值.
解答 解:∵|x+y-5|+(x-y+1)2=0,
∴$\left\{\begin{array}{l}{x+y=5}\\{x-y=-1}\end{array}\right.$,
则原式=(x+y)(x-y)=-5,
故答案为:-5
点评 此题考查了因式分解-运用公式法,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
10.在|-2|,0,1,-1这四个数中,最大的数是( )
| A. | |-2| | B. | 0 | C. | 1 | D. | -1 |
17.如图,是一组按照某种规律摆放成的图案,则图10中三角形的个数是( )


| A. | 100 | B. | 66 | C. | 36 | D. | 32 |
12. 如图,在数学课上,老师用5个完全相同的小长方形的无重叠的情况下拼成了一个大长方形,已知小长方形的长为3$\sqrt{10}$、宽为2$\sqrt{10}$,下列是四位同学对该大长方形的判断,其中不正确的是( )
如图,在数学课上,老师用5个完全相同的小长方形的无重叠的情况下拼成了一个大长方形,已知小长方形的长为3$\sqrt{10}$、宽为2$\sqrt{10}$,下列是四位同学对该大长方形的判断,其中不正确的是( )
 如图,在数学课上,老师用5个完全相同的小长方形的无重叠的情况下拼成了一个大长方形,已知小长方形的长为3$\sqrt{10}$、宽为2$\sqrt{10}$,下列是四位同学对该大长方形的判断,其中不正确的是( )
如图,在数学课上,老师用5个完全相同的小长方形的无重叠的情况下拼成了一个大长方形,已知小长方形的长为3$\sqrt{10}$、宽为2$\sqrt{10}$,下列是四位同学对该大长方形的判断,其中不正确的是( )| A. | 大长方形的长为6$\sqrt{10}$ | B. | 大长方形的宽为5$\sqrt{10}$ | ||
| C. | 大长方形的长为11$\sqrt{10}$ | D. | 大长方形的面积为300 |
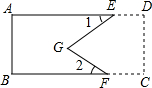 有一块长方形钢板ABCD,现将它加工成如图所示的零件,按规定∠1、∠2应分别为45°和30°.检验人员量得∠EGF为78°,就判断这个零件不合格,你能说明理由吗?
有一块长方形钢板ABCD,现将它加工成如图所示的零件,按规定∠1、∠2应分别为45°和30°.检验人员量得∠EGF为78°,就判断这个零件不合格,你能说明理由吗?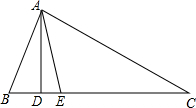 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求: 如图,∠A=30°,∠B=45°,∠C=40°,∠DFE=115°.
如图,∠A=30°,∠B=45°,∠C=40°,∠DFE=115°.