题目内容
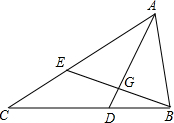 在△ABC中,AB<BC<CA,且AC-AB=2,D点在边BC上,且AD平分∠BAC.E为边AC上的一点,连接BE交AD于点G,且
在△ABC中,AB<BC<CA,且AC-AB=2,D点在边BC上,且AD平分∠BAC.E为边AC上的一点,连接BE交AD于点G,且| AC |
| CD |
| AE |
| BD |
| AG |
| GD |
| A、n=1 | B、n |
| C、n-1 | D、n-2 |
考点:平行线分线段成比例,三角形中位线定理
专题:
分析:过点E作EF∥AD 交CD于点F,根据平行线等分线段定理可以得出D是BF的中点,根据三角形的中位线定理即可求得BG=GE,根据垂直平分线的性质定理就可以求得AB=AE,进而求得CE=AC-AE=AC-AB=2,根据平行线等分线段定理即可得出
=
=
=2,从而得出CF=1,根据
=
=
=
,
=
=
=
得AE=n-1,进而求得BC=BD+DF+CF=2DF+CF=2×
+1=n.
| AE |
| DF |
| CE |
| CF |
| AC |
| CD |
| EF |
| AD |
| 2GD |
| AG+GD |
| 2 | ||
|
| 2 |
| n+1 |
| EF |
| AD |
| CE |
| AC |
| 2 |
| AE+CE |
| 2 |
| AE+2 |
| n-1 |
| 2 |
解答: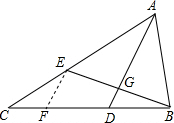 解:过点E作EF∥AD 交CD于点F,
解:过点E作EF∥AD 交CD于点F,
∴
=
,
∵
=
=2,
∴
=
,
∴BD=DF ①
∴DG为△BEF的中位线.
∴BG=GE
又∵∠BAG=∠EAG,
∴AB=AE,
∴CE=AC-AE=AC-AB=2
∵EF∥AD,
∴
=
=
=2,
∴DF=
,CF=1 ②
又∵
=
=
=
③
且∵
=
=
=
④
由③④两式得AE=n-1
由①②得BC=BD+DF+CF=2DF+CF=2×
+1=n.
故选B.
 解:过点E作EF∥AD 交CD于点F,
解:过点E作EF∥AD 交CD于点F,∴
| AC |
| AE |
| CD |
| DF |
∵
| AC |
| CD |
| AE |
| BD |
∴
| AC |
| AE |
| CD |
| BD |
∴BD=DF ①
∴DG为△BEF的中位线.
∴BG=GE
又∵∠BAG=∠EAG,
∴AB=AE,
∴CE=AC-AE=AC-AB=2
∵EF∥AD,
∴
| AE |
| DF |
| CE |
| CF |
| AC |
| CD |
∴DF=
| AE |
| 2 |
又∵
| EF |
| AD |
| 2GD |
| AG+GD |
| 2 | ||
|
| 2 |
| n+1 |
且∵
| EF |
| AD |
| CE |
| AC |
| 2 |
| AE+CE |
| 2 |
| AE+2 |
由③④两式得AE=n-1
由①②得BC=BD+DF+CF=2DF+CF=2×
| n-1 |
| 2 |
故选B.
点评:本题考查了平行线分线段成比例定理的运用,三角形的中位线性质定理的应用,线段的垂直平分线的性质定理,在解答时利用作平行线得出对应线段成比例是关键.

练习册系列答案
相关题目
 如图,在?ABCD中,BM=MC,AM交BD于点N,则BN:ND的值是( )
如图,在?ABCD中,BM=MC,AM交BD于点N,则BN:ND的值是( )| A、1:2 | B、1:2 |
| C、1:3 | D、2:1 |
下列语句:
①形状相同的三角形是全等三角形;
②有两边及一角对应相等的两个三角形全等;
③两个等边三角形一定全等;
④有两角一边对应相等的两个三角形全等.
其中错误的说法个数有( )
①形状相同的三角形是全等三角形;
②有两边及一角对应相等的两个三角形全等;
③两个等边三角形一定全等;
④有两角一边对应相等的两个三角形全等.
其中错误的说法个数有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
非负数a、b、c满足a+b-c=2,a-b+2c=1,则s=a+b+c的最大值与最小值的和为( )
| A、5 | B、9 | C、10 | D、12 |
 如图,AB为⊙O的直径,AB=10cm,动弦CD=6cm,动弦CD始终与AB相交,问当CD弦在⊙O上滑动时,A、B到直线CD距离之差的绝对值是否发生变化?若变化,请说明理由;若不变,予以证明并求其值.
如图,AB为⊙O的直径,AB=10cm,动弦CD=6cm,动弦CD始终与AB相交,问当CD弦在⊙O上滑动时,A、B到直线CD距离之差的绝对值是否发生变化?若变化,请说明理由;若不变,予以证明并求其值.