题目内容
(1)如图1,把两块全等的含45°的直角三角板ABC和DEF叠放在一起,使三角板DEF的锐角顶点E与三角板ABC的斜边中点重合.可知:△BPE∽△CEQ (不需说理)
(2)如图2,在(1)的条件下,把三角板ABC固定不动,让三角板DEF绕点E旋转,让三角板两边分别与线段BA的延长线、边AC的相交于点P、Q,连接PQ.
①若BC=4,设BP=x,CQ=y,则y与x的函数关系式为 ;
②写出图中能用字母表示的相似三角形 ;
③试判断∠BPE与∠EPQ的大小关系?并说明理由.
(3)如图3,在(2)的条件下,将三角板ABC改为等腰三角形,且AB=AC,三角板DEF改为一般三角形,其它条件不变,要使(2)中的结论③成立,猜想∠BAC与∠DEF关系为 .(将结论直接填在横线上)
(4)如图3,在(1)的条件下,将三角板ABC改为等腰三角形,且∠BAC=120°,AB=AC,三角板DEF改为∠DEF=30°直角三角形,把三角板ABC固定不动,让三角板DEF绕点E旋转,让三角板两边分别与线段BA的延长线、边AC的相交于点P、Q,连接PQ.若S△PEQ=2,PQ=2,求点C到AB的距离.
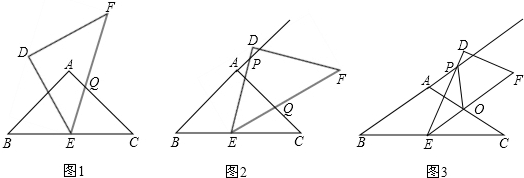
(2)如图2,在(1)的条件下,把三角板ABC固定不动,让三角板DEF绕点E旋转,让三角板两边分别与线段BA的延长线、边AC的相交于点P、Q,连接PQ.
①若BC=4,设BP=x,CQ=y,则y与x的函数关系式为
②写出图中能用字母表示的相似三角形
③试判断∠BPE与∠EPQ的大小关系?并说明理由.
(3)如图3,在(2)的条件下,将三角板ABC改为等腰三角形,且AB=AC,三角板DEF改为一般三角形,其它条件不变,要使(2)中的结论③成立,猜想∠BAC与∠DEF关系为
(4)如图3,在(1)的条件下,将三角板ABC改为等腰三角形,且∠BAC=120°,AB=AC,三角板DEF改为∠DEF=30°直角三角形,把三角板ABC固定不动,让三角板DEF绕点E旋转,让三角板两边分别与线段BA的延长线、边AC的相交于点P、Q,连接PQ.若S△PEQ=2,PQ=2,求点C到AB的距离.

考点:相似形综合题
专题:探究型
分析:(2)如图2,由(1)可知△BPE∽△CEQ,则有
=
=
,由BE=CE可得
=
,从而可证到△BPE∽△EPQ,则有△BPE∽△CEQ∽△EPQ.①利用相似三角形的性质就可得到y与x的关系;②由△ABC与△DEF全等可得△ABC∽△DEF,还有△BPE∽△CEQ∽△EPQ.③由△BPE∽△EPQ可得∠BPE=∠EPQ.
(3)若∠BAC+2∠DEF=180°,由AB=AC可得∠BAC+2∠B=180°,从而可得∠DEF=∠B,则有△BPE∽△EPQ,从而可得∠BPE=∠EPQ.
(4)过点E作EH⊥AB于H,点E作EG⊥PQ于G,点C作CN⊥AB于N,如图3.易得∠B=∠ACB=∠DEF,则有△BPE∽△EPQ,就可得到∠BPE=∠EPQ,根据角平分线的性质可得EH=EG.易证△BHE∽△BNC,从而得到CN=2EH=2EG.然后由S△PEQ=2,PQ=2可求出EG,就可得到点C到AB的距离.
| BP |
| CE |
| BE |
| CQ |
| EP |
| QE |
| BP |
| BE |
| EP |
| QE |
(3)若∠BAC+2∠DEF=180°,由AB=AC可得∠BAC+2∠B=180°,从而可得∠DEF=∠B,则有△BPE∽△EPQ,从而可得∠BPE=∠EPQ.
(4)过点E作EH⊥AB于H,点E作EG⊥PQ于G,点C作CN⊥AB于N,如图3.易得∠B=∠ACB=∠DEF,则有△BPE∽△EPQ,就可得到∠BPE=∠EPQ,根据角平分线的性质可得EH=EG.易证△BHE∽△BNC,从而得到CN=2EH=2EG.然后由S△PEQ=2,PQ=2可求出EG,就可得到点C到AB的距离.
解答:解:(2)如图2,
由(1)可知:△BPE∽△CEQ,
则有
=
=
.
∵BE=CE,∴
=
.
∵∠B=∠PEQ,
∴△BPE∽△EPQ.
∴△BPE∽△CEQ∽△EPQ.
①∵BE=CE=
BC=2,BP=x,CQ=y,
∴
=
,
∴y=
.
故答案为:y=
.
②∵△ABC与△DEF全等,∴△ABC∽△DEF.
故答案为:△BPE∽△CEQ∽△EPQ,△ABC∽△DEF.
③∠BPE=∠EPQ.
证明:∵△BPE∽△EPQ,∴∠BPE=∠EPQ.
(3)猜想:∠BAC+2∠DEF=180°.
理由如下:如图3,
∵AB=AC,∴∠B=∠ACB.
∵∠BAC+∠B+∠ACB=180°,
∴∠BAC+2∠B=180°,
∴∠DEF=∠B,
∴∠DEF=∠B=∠ACB,
则有△BPE∽△EPQ((2)中已证),
∴∠BPE=∠EPQ.
∴(2)中的结论③仍然成立.
故答案为:∠BAC+2∠DEF=180°.
(4)过点E作EH⊥AB于H,点E作EG⊥PQ于G,点C作CN⊥AB于N,如图3.
∵∠BAC=120°,AB=AC,
∴∠B=∠ACB=
=30°.
∵∠DEF=30°,∴∠B=∠ACB=∠DEF.
则有△BPE∽△EPQ((2)中已证),
∴∠BPE=∠EPQ.
∵EH⊥AB,EG⊥PQ,
∴EH=EG.
∵EH⊥AB,CN⊥AB,
∴EH∥CN,
∴△BHE∽△BNC,
∴
=
=
.
∴CN=2EH.
∴CN=2EG.
∵S△PEQ=
PQ•EG=2,PQ=2,
∴EG=2,
∴CN=4.
∴点C到AB的距离为4.
由(1)可知:△BPE∽△CEQ,
则有
| BP |
| CE |
| BE |
| CQ |
| EP |
| QE |

∵BE=CE,∴
| BP |
| BE |
| EP |
| QE |
∵∠B=∠PEQ,
∴△BPE∽△EPQ.
∴△BPE∽△CEQ∽△EPQ.
①∵BE=CE=
| 1 |
| 2 |
∴
| x |
| 2 |
| 2 |
| y |
∴y=
| 4 |
| x |
故答案为:y=
| 4 |
| x |
②∵△ABC与△DEF全等,∴△ABC∽△DEF.
故答案为:△BPE∽△CEQ∽△EPQ,△ABC∽△DEF.
③∠BPE=∠EPQ.
证明:∵△BPE∽△EPQ,∴∠BPE=∠EPQ.
(3)猜想:∠BAC+2∠DEF=180°.
理由如下:如图3,
∵AB=AC,∴∠B=∠ACB.
∵∠BAC+∠B+∠ACB=180°,
∴∠BAC+2∠B=180°,

∴∠DEF=∠B,
∴∠DEF=∠B=∠ACB,
则有△BPE∽△EPQ((2)中已证),
∴∠BPE=∠EPQ.
∴(2)中的结论③仍然成立.
故答案为:∠BAC+2∠DEF=180°.
(4)过点E作EH⊥AB于H,点E作EG⊥PQ于G,点C作CN⊥AB于N,如图3.
∵∠BAC=120°,AB=AC,
∴∠B=∠ACB=
| 180°-120° |
| 2 |
∵∠DEF=30°,∴∠B=∠ACB=∠DEF.
则有△BPE∽△EPQ((2)中已证),
∴∠BPE=∠EPQ.
∵EH⊥AB,EG⊥PQ,
∴EH=EG.
∵EH⊥AB,CN⊥AB,
∴EH∥CN,
∴△BHE∽△BNC,
∴
| EH |
| CN |
| BE |
| BC |
| 1 |
| 2 |
∴CN=2EH.
∴CN=2EG.
∵S△PEQ=
| 1 |
| 2 |
∴EG=2,
∴CN=4.
∴点C到AB的距离为4.
点评:本题主要考查了相似三角形的判定与性质、等腰三角形的性质、角平分线的性质、三角形的内角和定理、三角形的面积等知识,突出对K型相似模型(由∠B=∠C=∠PEQ可得△BPE∽△CEQ,由∠B=∠C=∠PEQ,BE=CE可得△BPE∽△CEQ∽△EPQ)的考查,应熟悉并掌握它.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
从数列1,2,3,4,…,500中去除一些数,组成一个新数列,要求这个新数列中的任意两个数之和都不是7的倍数,则这个新数列中最大的数是( )
| A、216 | B、217 |
| C、213 | D、287 |
张贝把一个多项式分解因式时,得到的正确结果是三个不同整式,其中有两个是m和(a-b),你认为第三个可能是( )
| A、m(a-b) | B、a-b |
| C、m | D、a+b |
非负数a、b、c满足a+b-c=2,a-b+2c=1,则s=a+b+c的最大值与最小值的和为( )
| A、5 | B、9 | C、10 | D、12 |
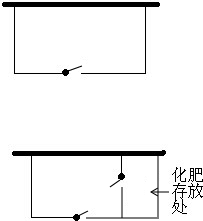 张大爷用32米长的篱笆围成一个矩形菜园,菜园一边靠墙(墙长为15米),平行于墙的一面开一扇宽度为2米的门(如图1).(注:门都用其它材料)
张大爷用32米长的篱笆围成一个矩形菜园,菜园一边靠墙(墙长为15米),平行于墙的一面开一扇宽度为2米的门(如图1).(注:门都用其它材料)