题目内容
8.若3xa+b-2ya-b=5是关于x、y的二元一次方程,则ab=0.分析 利用二元一次方程的定义判断即可.
解答 解:∵3xa+b-2ya-b=5是关于x、y的二元一次方程,
∴$\left\{\begin{array}{l}{a+b=1}\\{a-b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$,
则ab=0,
故答案为:0
点评 此题考查了二元一次方程的定义,熟练掌握二元一次方程的定义是解本题的关键.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
19.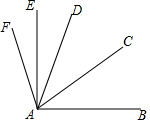 如图,∠FAB=106°,AE是∠FAD的平分线,AC是∠DAB的平分线,∠EAD=20°.下列关系错误的是( )
如图,∠FAB=106°,AE是∠FAD的平分线,AC是∠DAB的平分线,∠EAD=20°.下列关系错误的是( )
 如图,∠FAB=106°,AE是∠FAD的平分线,AC是∠DAB的平分线,∠EAD=20°.下列关系错误的是( )
如图,∠FAB=106°,AE是∠FAD的平分线,AC是∠DAB的平分线,∠EAD=20°.下列关系错误的是( )| A. | ∠FAD=40° | B. | ∠CAB=33° | C. | ∠FAB=2∠EDC | D. | ∠EAD与∠DAB互余 |
13.邮递员从山坡下的邮局出发,骑自行车到达山坡顶后,停下一段时间分发邮件,之后沿原路返回邮局,设邮递员从邮局出发后所用的时间为x(分钟),邮递员与邮局的距离为y(米),则y与x的函数图象大致是( )
| A. | 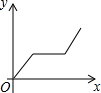 | B. | 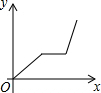 | C. | 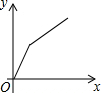 | D. | 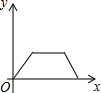 |
20.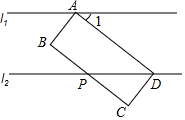 如图,分别过矩形ABCD的顶点A、D作直线l1、l2,使l1∥l2,l2与边BC交于点P,若∠1=38°,则∠BPD为( )
如图,分别过矩形ABCD的顶点A、D作直线l1、l2,使l1∥l2,l2与边BC交于点P,若∠1=38°,则∠BPD为( )
 如图,分别过矩形ABCD的顶点A、D作直线l1、l2,使l1∥l2,l2与边BC交于点P,若∠1=38°,则∠BPD为( )
如图,分别过矩形ABCD的顶点A、D作直线l1、l2,使l1∥l2,l2与边BC交于点P,若∠1=38°,则∠BPD为( )| A. | 162° | B. | 152° | C. | 142° | D. | 128° |
17.已知∠C=75°,则∠A与∠B满足以下哪个选项才能构成△ABC( )
| A. | sinA=$\frac{\sqrt{2}}{2}$,sinB=$\frac{\sqrt{2}}{2}$ | B. | cosA=$\frac{1}{2}$,cosB=$\frac{\sqrt{3}}{2}$ | C. | sinA=$\frac{\sqrt{2}}{2}$,tanB=$\sqrt{3}$ | D. | sinA=$\frac{\sqrt{3}}{2}$,cosB=$\frac{1}{2}$ |
 如图,△DEF是由△ABC平移而得到的,并且BC=11,EC=6,AB=15,则CF的长为( )
如图,△DEF是由△ABC平移而得到的,并且BC=11,EC=6,AB=15,则CF的长为( ) 一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是记.
一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是记.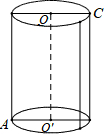 如图,有一个圆柱,它的高等于8cm,底面半径等于5cm,在圆柱的下底面点A处有一只蚂蚁,它想吃到上底面与点A相对的点C处的食物,需要爬行的最短路是多少?(π的值取3)
如图,有一个圆柱,它的高等于8cm,底面半径等于5cm,在圆柱的下底面点A处有一只蚂蚁,它想吃到上底面与点A相对的点C处的食物,需要爬行的最短路是多少?(π的值取3)