题目内容
17.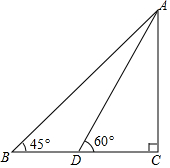 如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)
如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)
分析 Rt△ABC中知AC=BC=ABcosB=3$\sqrt{3}$,再在Rt△ACD中由CD=$\frac{AC}{tan∠ADC}$=3可得BD=BC-CD≈2.196,继而可作出判断.
解答 解:在Rt△ABC中,∵AB=3$\sqrt{6}$,∠B=45°,
∴AC=BC=ABcosB=3$\sqrt{6}$×$\frac{\sqrt{2}}{2}$=3$\sqrt{3}$,
在Rt△ACD中,∵∠ADC=60°,
∴CD=$\frac{AC}{tan∠ADC}$=$\frac{3\sqrt{3}}{\sqrt{3}}$=3,
则BD=BC-CD=3$\sqrt{3}$-3≈2.196,
∴改造后斜坡前方的空地长度为3+2.196=5.196<6,
∴进行这样的改造不可行.
点评 本题主要考查解直角三角形的应用-坡度坡角问题,利用这两个直角三角形有公共的直角边求解是解决此类题目的基本出发点.

练习册系列答案
相关题目
7. 如图,∠ADE=∠ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC等于( )
如图,∠ADE=∠ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC等于( )
 如图,∠ADE=∠ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC等于( )
如图,∠ADE=∠ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC等于( )| A. | 12 | B. | 15 | C. | 18 | D. | 20 |
6.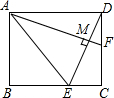 如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )
如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )
 如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )
如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )| A. | $\sqrt{15}$ | B. | $\frac{{\sqrt{15}}}{15}$ | C. | 1 | D. | $\frac{{\sqrt{15}}}{10}$ |
4.从达州开往成都的D5199次列车平均提速30km/h,用相同的时间,这列车提速前行驶200km,提速后比提速前多行驶80km,设提速前列车的平均速度为xkm/h,下列方程正确的是( )
| A. | $\frac{200}{x}$=$\frac{200-80}{x+30}$ | B. | $\frac{200}{x}$=$\frac{200-80}{x-30}$ | C. | $\frac{200}{x}$=$\frac{200+80}{x-30}$ | D. | $\frac{200}{x}$=$\frac{200+80}{x+30}$ |
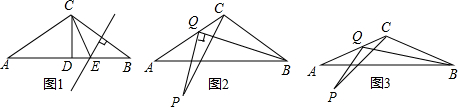
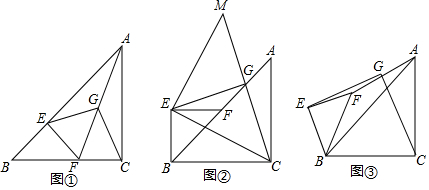
 如图,∠ABC=∠ACB.∠ABC、∠ACB的平分线分别交AC、AB于点D、E,且∠1=∠2,试说明CE∥DF.
如图,∠ABC=∠ACB.∠ABC、∠ACB的平分线分别交AC、AB于点D、E,且∠1=∠2,试说明CE∥DF. 如图,一次函数y1=x+1的图象与x轴交于点A,与反比例函数y2=$\frac{k}{x}$的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.
如图,一次函数y1=x+1的图象与x轴交于点A,与反比例函数y2=$\frac{k}{x}$的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.