题目内容
10.点F在线段AB上,点E在线段CD上,点P是平面内一点(1)如图1,若∠FPE-∠BFP=∠DEP,求证:AB∥CD;
(2)在(1)条件下,∠BFP和∠DEP的平分线相交于点H,过点E作EQ⊥EH交∠AFP的角平分线于点Q,连接PQ,且PQ∥FH,若∠FHE=35°,∠QEC=80°,求∠QPE的度数.

分析 (1)过P作PM∥AB,根据平行线的性质得到∠BFP=∠FPM,等量代换得到∠MPE=∠PED,根据平行线的判定定理即可得到结论;
(2)由(1)可得∠H=∠BFH+∠DEH=35°,∠FQE=∠AFQ+∠CEQ,根据角平分线的定义得到∠PEH=∠DEH根据余角的性质得到∠CEQ=∠PEQ,然后根据角的和差即可得到结论.
解答 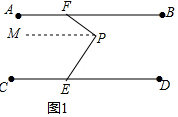 解:(1)过P作PM∥AB,
解:(1)过P作PM∥AB,
∴∠BFP=∠FPM,
∴∠MPE=∠FPE-∠BFP,
∵∠FPE-∠BFP=∠DEP,
∴∠MPE=∠PED,
∴CD∥PM,
∴AB∥CD;
(2)由(1)可得:∠H=∠BFH+∠DEH=35°,∠FQE=∠AFQ+∠CEQ,
∵∠QEC=80°,
∵HE平分∠PED,
∴∠PEH=∠DEH,∵QE⊥EH,
∴∠CEQ+∠HED=∠QEP+∠PEH=90°,
∴∠CEQ=∠PEQ,
∵∠QEC=80°,
∴∠HED=10°,
∴∠BFH=25°,
∴∠BFP=50°,∠PED=20°,
∴∠AFQ=65°,
∴∠FQE=145°,
∴∠PQE=55°,
∵∠QEP=80°,
∴∠QPE=45°.
点评 本题考查了平行线的判定和性质,余角的性质,角平分线的定义,熟练掌握平行线的判定和性质是解题的关键.

练习册系列答案
相关题目
5.如果一个多边形的每一个内角都是135°,那么这个多边形的边数是( )
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
 如图,在△BCE中,AC⊥BE,AB=AC,点A、点F分别在BE、CE上,BE、CF相交于点D,BD=CE.求证:AD=AE.
如图,在△BCE中,AC⊥BE,AB=AC,点A、点F分别在BE、CE上,BE、CF相交于点D,BD=CE.求证:AD=AE.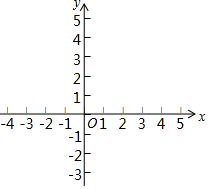 在如图所示的平面直角坐标系中作出y=-x+3和y=2x+6的图象并求两直线的交点坐标.
在如图所示的平面直角坐标系中作出y=-x+3和y=2x+6的图象并求两直线的交点坐标. 如图,在菱形ABCD中,∠BAD=60°.求$\frac{BD}{AC}$的值.
如图,在菱形ABCD中,∠BAD=60°.求$\frac{BD}{AC}$的值.