题目内容

18．如图，在△BCE中，AC⊥BE，AB=AC，点A、点F分别在BE、CE上，BE、CF相交于点D，BD=CE．求证：AD=AE．

分析 利用“HL”证明Rt△ABD和Rt△ACE全等，根据全等三角形对应边相等证明即可．

解答 证明：∵AC⊥BE，
∴∠BAD=∠CAE=90°，
在Rt△ABD和Rt△ACE中，$\left\{\begin{array}{l}{BD=CE}\\{AB=AC}\end{array}\right.$，
∴Rt△ABD≌Rt△ACE（HL），
∴AD=AE．

点评 本题考查了全等三角形的判定与性质，熟练掌握三角形全等的判定方法并准确识图确定出全等三角形是解题的关键．

练习册系列答案
相关题目
8．t2-（t+1）（t-5）的计算结果正确的是（　　）
A．-4t-5B．4t+5C．t2-4t+5D．t2+4t-5
9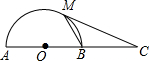．如图，AB为⊙O的直径，P点在AB延长线上，PM切⊙O于M点，若OA=a，PM=$\sqrt{3}$a，那么△PMB的周长为（　　）
A．2aB．2$\sqrt{3}$aC．aD．（2+$\sqrt{3}$）a
6．a、b为常数，关于x的方程$\frac{2kx+a}{3}$=2+$\frac{x-bk}{6}$，无论k为何值，它的解总是1，则2a+b=9．
13．用简便方法计算：
（1）$（-\frac{1}{3}+\frac{2}{9}-\frac{5}{12}）÷（-\frac{1}{36}）$     
（2）$（+6\frac{3}{5}）+（-5\frac{2}{3}）+（4\frac{2}{5}）+（-1\frac{1}{3}）$   
（3）$（-8）×9×（-1.25）×（-\frac{1}{9}）$  
（4）$（-24\frac{34}{35}）×2.5×（-8）$．
3．将下列各数填在相应的集合里．
-$\frac{2}{3}$，9，0，+4.3，|-0.5|，-（+7），18%，（-3）4，-（-2）5，-62
正有理数集合：{                                            …}；
正分数集合：{                                              …}；
负整数集合：{                                              …}；
自然数集合：{                                              …}．
10．点F在线段AB上，点E在线段CD上，点P是平面内一点
（1）如图1，若∠FPE-∠BFP=∠DEP，求证：AB∥CD；
（2）在（1）条件下，∠BFP和∠DEP的平分线相交于点H，过点E作EQ⊥EH交∠AFP的角平分线于点Q，连接PQ，且PQ∥FH，若∠FHE=35°，∠QEC=80°，求∠QPE的度数．
7．如图，点M是矩形ABCD的边AD的中点．点P是BC边上一动点，PE⊥MC，PF⊥BM．垂足为E、F．
（1）当AD=2AB时．求证：四边形PEMF为矩形；
（2）在（1）的条件下．当点P运动到什么位置时．矩形PEMF变为正方形．为什么!
4．已知，如图，在△ABC中：
（1）如图①，∠ABC、∠ACB的角平分线交于点O，若∠A=60°，则∠BOC的度数为120°；
（2）如图②，∠ABC、∠ACB的三等分线分别对应交于O1、O2，当∠BO2C=2∠A时，求∠A的度数；
（3）如图③，∠ABC、∠ACB的n等分线分别对应交于O1、O2…On-1，当∠BOn-1C=2∠A时，猜想：∠A的度数为$\frac{180°}{n+1}$（用含n的代数式表示）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网