题目内容
16.已知关于x的方程x2-2(m+1)x+m2-1=0有两个不相等的实数根x1,x2.(1)求实数m的取值范围;
(2)当m取最小整数时,求2x12-2x1+x22的值;
(3)若抛物线y=x2-2(m+1)x+m2-1与y轴的负半轴交于点C,与x轴交于点A,B,且∠ACB=90°,求m的值.
分析 (1)直接用一元二次方程根的判别式判断即可;
(2)先借助(1)的结论得出m=0,代入方程再利用根与系数的关系即可;
(3)先求出点C的坐标和AB的中点坐标,即可得出CD,利用直角三角形斜边的中线等于斜边的一半即可求出m.
解答 解:(1)依题意,有:△=4(m+1)2-4(m2-1)>0,
即 2m+2>0,
得 m>-1.
(2)∵m>-1,
∴m取最小整数为0.当m=0时,原方程变为 x2-2x-1=0.
∵x1是x2-2x-1=0的根,
∴x12-2x1-1=0,即x12-2x1=1.
又∵x1,x2是方程x2-2x-1=0的两个根,
∴x1+x2=2,x1x2=-1.
∴2x12-2x1+x22=x12-2x1+x12+x22=1+x12+x22=1+(x1+x2)2-2 x1x2=1+4-2×(-1)=7.
(3)∵抛物线y=x2-2(m+1)x+m2-1与y轴的负半轴交于点C,
∴C(0,m2-1),
∵抛物线y=x2-2(m+1)x+m2-1,
∴AB的坐标为D(m+1,0),
∴CD=$\sqrt{(m+1)^{2}+({m}^{2}-1)^{2}}$=(m+1)$\sqrt{{m}^{2}-2m+2}$
∵x2-2(m+1)x+m2-1=0,
∴x1+x2=2(m+1),x1x2=m2-1,
∴AB=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=2$\sqrt{2m+2}$,
∵∠ACB=90°,
∴CD=$\frac{1}{2}$AB,
∴(m+1)$\sqrt{{m}^{2}-2m+2}$=$\sqrt{2m+2}$,
∴m=0或m=1,
∵抛物线y=x2-2(m+1)x+m2-1与y轴的负半轴交于点C,
∴m2-1<0,
∴-1<m<1,
∴m=0.
点评 此题是二次函数综合题,主要考查了一元二次方程根的判别式,根与系数的关系,灵活运用根与系数的关系是解本题的关键.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | 12a3y与$\frac{2ya^3}{3}$ | B. | 6a2mb与-a2bm | C. | 23与32 | D. | $\frac{1}{2}$x3y与-$\frac{1}{2}$xy3 |


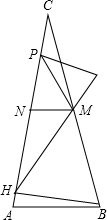 如图,△ABC中,M,N分别是BC,AC的中点,BH是AC边上的高线,∠HMN=45°,MP垂直∠HMN的平分线并交AC于点P,若PH=$\frac{1}{2}$(AB+BC),求证:△ABC是等腰三角形.
如图,△ABC中,M,N分别是BC,AC的中点,BH是AC边上的高线,∠HMN=45°,MP垂直∠HMN的平分线并交AC于点P,若PH=$\frac{1}{2}$(AB+BC),求证:△ABC是等腰三角形. 如图:在△ABC中,∠C=90°,点D是AB边上一点,DM⊥AB且DE=BC,过点M作ME∥BC交AB于点E.求证:ME=AB.
如图:在△ABC中,∠C=90°,点D是AB边上一点,DM⊥AB且DE=BC,过点M作ME∥BC交AB于点E.求证:ME=AB.