题目内容
12.化简:$\root{3}{{a}^{\frac{1}{2}}\sqrt{{a}^{-3}}}$÷$\sqrt{\root{3}{{a}^{-8}}•\root{3}{{a}^{15}}}$÷$\root{3}{\sqrt{{a}^{-3}}•\sqrt{{a}^{-1}}}$(a>0)分析 首先根据一个数的平方根、立方根的方法,分别求出$\root{3}{{a}^{\frac{1}{2}}\sqrt{{a}^{-3}}}$、$\sqrt{\root{3}{{a}^{-8}}•\root{3}{{a}^{15}}}$、$\root{3}{\sqrt{{a}^{-3}}•\sqrt{{a}^{-1}}}$的值各是多少;然后从左向右依次计算,求出算式的值是多少即可.
解答 解:$\root{3}{{a}^{\frac{1}{2}}\sqrt{{a}^{-3}}}$÷$\sqrt{\root{3}{{a}^{-8}}•\root{3}{{a}^{15}}}$÷$\root{3}{\sqrt{{a}^{-3}}•\sqrt{{a}^{-1}}}$
=$\root{3}{{a}^{-1}}$÷$\sqrt{{a}^{\frac{7}{3}}}$÷$\root{3}{{a}^{-2}}$
=${a}^{-\frac{1}{3}}$${÷a}^{\frac{7}{6}}$÷${a}^{-\frac{2}{3}}$
=${a}^{-\frac{5}{6}}$.
点评 此题主要考查了分数指数幂,要熟练掌握,解答此题的关键是要明确求一个数的平方根、立方根的方法.

练习册系列答案
相关题目
2. 如图,四边形ABCD中,AB=CD,对角线AC,BD交于点O,下列条件中,不能说明四边形ABCD是平行四边形的是( )
如图,四边形ABCD中,AB=CD,对角线AC,BD交于点O,下列条件中,不能说明四边形ABCD是平行四边形的是( )
 如图,四边形ABCD中,AB=CD,对角线AC,BD交于点O,下列条件中,不能说明四边形ABCD是平行四边形的是( )
如图,四边形ABCD中,AB=CD,对角线AC,BD交于点O,下列条件中,不能说明四边形ABCD是平行四边形的是( )| A. | AD=BC | B. | AC=BD | C. | AB∥CD | D. | ∠BAC=∠DCA |
 如图,在?ABCD中,已知AD=10cm,AB=6cm,AE平分∠BAD交BC边于E,则EC的长为4cm.
如图,在?ABCD中,已知AD=10cm,AB=6cm,AE平分∠BAD交BC边于E,则EC的长为4cm. 二次函数y=ax2+bx的图象如图所示,那么一次函数y=ax+b的图象大致是( )
二次函数y=ax2+bx的图象如图所示,那么一次函数y=ax+b的图象大致是( )



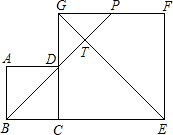 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为2$\sqrt{2}$.
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为2$\sqrt{2}$. 如图,△ABC中,∠ABC的外角平分线BD与∠ACB外角平分线CE相交于点P,求证:点P到三边AB、BC、CA所在直线的距离相等.
如图,△ABC中,∠ABC的外角平分线BD与∠ACB外角平分线CE相交于点P,求证:点P到三边AB、BC、CA所在直线的距离相等.