题目内容
8.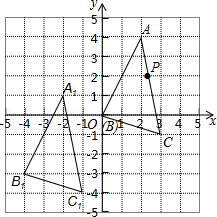 在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2.
在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2.(1)说明△A1B1C1是由△ABC经过怎样的平移得到的?
(2)直接写出点P2的坐标;
(3)计算△A1B1C1的面积.
分析 (1)直接利用平移的性质结合对应点移动的位置得出平移规律;
(2)利用已知平移规律得出P1坐标,再利用旋转的性质得出P2点坐标;
(3)利用△A1B1C1所在矩形面积减去周围三角形面积进而得出答案.
解答  解:(1)如图所示:
解:(1)如图所示:
△ABC先向下平移3个单位,再向左平移4个单位得到△A1B1C1;
(2)∵点P(2.4,2)平移后的对应点为P1,
∴P1(-1.6,-1),
∵点P1绕点O逆时针旋转180°,得到对应点P2,
∴P2(1.6,1);
(3)△A1B1C1的面积为:3×5-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×5-$\frac{1}{2}$×1×3=7.
点评 此题主要考查了平移变换以及旋转变换和三角形面积求法,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
16.下列说法错误的是( )
| A. | 经过平移,对应点所连的线段平行且相等 | |
| B. | 经过平移,对应线段平行 | |
| C. | 平移中,图形上每个点移动的距离可以不同 | |
| D. | 平移不改变图形的形状和大小 |
3.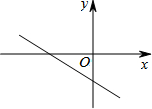 如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a的取值范围是( )
如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a的取值范围是( )
 如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a的取值范围是( )
如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a的取值范围是( )| A. | a>0 | B. | -3<a<0 | C. | a<-3 | D. | a<0 |
11.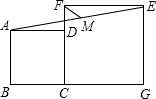 如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B、C、G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为( )
如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B、C、G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为( )
 如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B、C、G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为( )
如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B、C、G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$ |
