题目内容
20.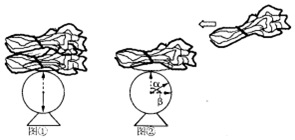 王老师到菜市场买菜,发现若把10千克的菜放到某秤上,秤的指针盘上的指针转了,如图①所示;于是王老师在学完一元一次方程和角的相关知识后给学生提出了两个问题:
王老师到菜市场买菜,发现若把10千克的菜放到某秤上,秤的指针盘上的指针转了,如图①所示;于是王老师在学完一元一次方程和角的相关知识后给学生提出了两个问题:(1)王老师把6千克的菜放在该秤上,指针转过多少度?
(2)若刘大妈第一次把x千克的菜放在秤上,通过指针盘读数发现与自己所需数量还差一些,于是再放了1千克的菜上去,发现前、后两次指针转过的角度α与β恰好互余.如图②,试问x的值是多少?
分析 (1)算出秤上放1千克菜转过的角度为多少,乘以6即可;
(2)利用两次角度的和等于90°列出方程求解即可.
解答 解:(1)由已知得:老师把6千克的菜放在该秤上,指针转过的度数为:$\frac{180°}{10}$×6=108°.
(2)设刘大妈第一次放x千克菜在秤盘上,
则$\frac{180°}{10}$•x+$\frac{180°}{10}$=90°,
解得x=4.
故:刘大妈第一次放4千克菜在秤盘上.
点评 本题考查了一元一次方程的应用,解决本题的关键是得到秤上放1千克菜转过的角度为多少.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
10.$\sqrt{26}$-2的值在( )
| A. | 2、3之间 | B. | 3、4之间 | C. | 5、6之间 | D. | 6、7之间 |
8.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{7}$=$\sqrt{10}$ | B. | 7$\sqrt{7}$-2$\sqrt{2}$=5$\sqrt{5}$ | C. | 2$\sqrt{2}$×3$\sqrt{2}$=6$\sqrt{2}$ | D. | $\sqrt{2}$÷$\sqrt{5}$=$\frac{\sqrt{10}}{5}$ |
15.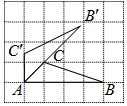 如图,△ABC的三个顶点都在正方形网格的格点处,若将△ABC绕点A逆时针旋转得到△A′B′C′,则tanB′的值为( )
如图,△ABC的三个顶点都在正方形网格的格点处,若将△ABC绕点A逆时针旋转得到△A′B′C′,则tanB′的值为( )
 如图,△ABC的三个顶点都在正方形网格的格点处,若将△ABC绕点A逆时针旋转得到△A′B′C′,则tanB′的值为( )
如图,△ABC的三个顶点都在正方形网格的格点处,若将△ABC绕点A逆时针旋转得到△A′B′C′,则tanB′的值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
12.下列事件中,必然事件是( )
| A. | 掷一枚硬币,正面朝上 | |
| B. | 从2、4、6、8、10这5张卡片中任抽一张是奇数 | |
| C. | a是实数,|a|≥0 | |
| D. | 从车间刚生产的产品中任意抽取一件,是次品 |
 如图,∠1=13°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为103°.
如图,∠1=13°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为103°.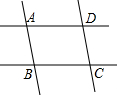 如图,①如果AD∥BC,那么根据两直线平行,同旁内角互补,得∠BAD+∠ABC=180°;②如果AB∥CD,那么根据两直线平行,同旁内角互补,得∠BCD+∠ABC=180°.
如图,①如果AD∥BC,那么根据两直线平行,同旁内角互补,得∠BAD+∠ABC=180°;②如果AB∥CD,那么根据两直线平行,同旁内角互补,得∠BCD+∠ABC=180°.