题目内容
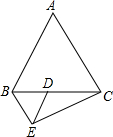 已知:如图,△ABC和△BDE均为等边三角形,B、D、C三点在一条直线上,AC⊥CE,判断线段DE与AC的数量关系,并加以证明.
已知:如图,△ABC和△BDE均为等边三角形,B、D、C三点在一条直线上,AC⊥CE,判断线段DE与AC的数量关系,并加以证明.判断:
证明:
考点:等边三角形的性质,含30度角的直角三角形
专题:探究型
分析:根据等边三角形的性质,由△ABC为等边三角形得到AC=BC,∠ACB=60°,则由AC⊥CE可计算出∠BCE=30°,再利用△BDE为等边三角形得到DE=BE,∠DBE=60°,于是根据三角形内角和定理可计算出∠BEC=90°,然后在Rt△BEC中利用含30度的直角三角形三边的关系可得BE=
BC,所以DE=
AC.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:DE=
AC.
证明如下:∵△ABC为等边三角形,
∴AC=BC,∠ACB=60°,
∵AC⊥CE,
∴∠ACE=90°,
∴∠BCE=90°-60°=30°,
∵△BDE为等边三角形,
∴DE=BE,∠DBE=60°,
∴∠BEC=180°-60°-30°=90°,
在Rt△BEC中,∵∠BCE=30°,
∴BE=
BC,
∴DE=
AC.
故答案为DE=
AC.
| 1 |
| 2 |
证明如下:∵△ABC为等边三角形,
∴AC=BC,∠ACB=60°,
∵AC⊥CE,
∴∠ACE=90°,
∴∠BCE=90°-60°=30°,
∵△BDE为等边三角形,
∴DE=BE,∠DBE=60°,
∴∠BEC=180°-60°-30°=90°,
在Rt△BEC中,∵∠BCE=30°,
∴BE=
| 1 |
| 2 |
∴DE=
| 1 |
| 2 |
故答案为DE=
| 1 |
| 2 |
点评:本题考查了等边三角形的性质:等边三角形的三个内角都相等,且都等于60°.也考查了含30度的直角三角形三边的关系.

练习册系列答案
相关题目
若关于x的分式方程
=1的解是非正数,则a的取值范围是( )
| a+2 |
| x+1 |
| A、a<1 | B、a≥1 |
| C、a≤-1 | D、a≤-1且a≠-2 |
 如图,⊙O是△ABC的内切圆,D、E、F分别是切点,判定△DEF的形状(按角分类),并说明理由.
如图,⊙O是△ABC的内切圆,D、E、F分别是切点,判定△DEF的形状(按角分类),并说明理由.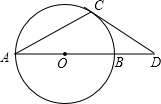 如图:已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10.
如图:已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10.