题目内容
某是出租车收费标准如下:3km以内(含3km)收费11元,3km至10km每km收费3元;10km以上每km收费4元.(不足1km以1km计算)
(1)小明家距离学校12.3km,某个周末,小明身边带了39元钱,问:小明从学习哦啊坐出租车到家的钱够吗?如果够,还剩多少钱?如果不够,他至少要先走多少km路?
(2)某天,小明和爸爸分别从不同的地方坐出租车回家,结果正好同时到家,且正好都行了整km,父子俩一合计,方向两人共形20km,共付车费67元,已知小明的行程超过10km,而父亲的行程在3km到10km之间,两人各行了多少km?
(1)小明家距离学校12.3km,某个周末,小明身边带了39元钱,问:小明从学习哦啊坐出租车到家的钱够吗?如果够,还剩多少钱?如果不够,他至少要先走多少km路?
(2)某天,小明和爸爸分别从不同的地方坐出租车回家,结果正好同时到家,且正好都行了整km,父子俩一合计,方向两人共形20km,共付车费67元,已知小明的行程超过10km,而父亲的行程在3km到10km之间,两人各行了多少km?
考点:一元一次方程的应用
专题:
分析:(1)设小明身边带了39元钱可以走xkm,建立方程求出x的值与12.3km作比较就可以得出结论;
(2)设小明行驶了a千米,则小明爸爸行驶了(20-a)千米,根据两人的总费用=67元建立方程求出其解即可.
(2)设小明行驶了a千米,则小明爸爸行驶了(20-a)千米,根据两人的总费用=67元建立方程求出其解即可.
解答:解:(1)设小明身边带了39元钱可以走xkm,由题意,得
11+3×(10-3)+4(x-10)=39,
解得:x=
,
∵
<12.3,
∴小明的钱不够,
∴他至少要先走12.3-
=0.55km的路;
(2)设小明行驶了a千米,则小明爸爸行驶了(20-a)千米,由题意,得
11+21+4(a-10)+11+3(20-a-3)=67,
解得:a=13.
则小明爸爸行驶的路程为:20-13=7千米.
答:小明行驶了13千米,小明的爸爸行驶了7千米.
11+3×(10-3)+4(x-10)=39,
解得:x=
| 47 |
| 4 |
∵
| 47 |
| 4 |
∴小明的钱不够,
∴他至少要先走12.3-
| 47 |
| 4 |
(2)设小明行驶了a千米,则小明爸爸行驶了(20-a)千米,由题意,得
11+21+4(a-10)+11+3(20-a-3)=67,
解得:a=13.
则小明爸爸行驶的路程为:20-13=7千米.
答:小明行驶了13千米,小明的爸爸行驶了7千米.
点评:本题考查了列一元一次方程解实际问题的运用,一元一次方程的解法的运用,行程问题的数量关系运用,解答时由行程问题的数量关系建立方程是关键.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
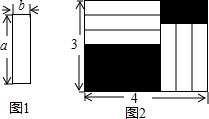 如图1是长为a,宽为b的小长方形卡片,把六张这样的小长方形卡片不重叠地放在一个底面为长方形(长为4,宽为3)的盒子底部(如图2),盒子底部未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长之和为( )
如图1是长为a,宽为b的小长方形卡片,把六张这样的小长方形卡片不重叠地放在一个底面为长方形(长为4,宽为3)的盒子底部(如图2),盒子底部未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长之和为( )| A、8 | B、10 | C、12 | D、14 |
甲、乙、丙三辆车均在A、B两地间往返,三辆车在A、B两地间往返一次所需时间分别为5小时、3小时和2小时.现在三辆车同时在A地视为第一次汇合,甲车先出发,1 小时后乙车出发,再经过2小时后丙车出发.那么丙车出发( )小时后,三辆车第三次同时汇合于A地.
| A、50 | B、51 | C、52 | D、53 |
已知
=
=
,且3x-2y+z≠0,则
=( )
| x |
| 3 |
| y |
| 5 |
| z |
| 7 |
| 3x+2y-z |
| 3x-2y+z |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
根据等式性质5=3x-2可变形为( )
| A、-3x=2-5 |
| B、-3x=-2+5 |
| C、5-2=3x |
| D、-3x=-5-2 |
 将△ABC绕点A按逆时针旋转30°后,得到△ADC′,则∠ABD的度数是
将△ABC绕点A按逆时针旋转30°后,得到△ADC′,则∠ABD的度数是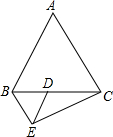 已知:如图,△ABC和△BDE均为等边三角形,B、D、C三点在一条直线上,AC⊥CE,判断线段DE与AC的数量关系,并加以证明.
已知:如图,△ABC和△BDE均为等边三角形,B、D、C三点在一条直线上,AC⊥CE,判断线段DE与AC的数量关系,并加以证明.