题目内容
7.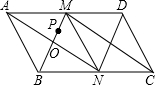 如图所示,在平行四边形ABCD中,M,N分别是AD,BC的中点,∠BMC=90°,连接AN,DN,AN与BM交于点O.
如图所示,在平行四边形ABCD中,M,N分别是AD,BC的中点,∠BMC=90°,连接AN,DN,AN与BM交于点O.(1)求证:△ABM≌△CDN;
(2)点P在直线BM上,若BM=3,CM=4,求△PND的周长的最小值.
分析 (1)根据判定定理(SAS)进行判定.
(2)只需求得PN+PD的最短距离即可.即只需证明:点A与点N关于直线BM对称,故当点P与点M重合时,△PND的周长最小.
解答 (1)证明:∵四边形ABCD是平行四边形,M,N分别是AD,BC的中点,
∴AM=CN,AB=CD,∠BAM=∠NCD
∴在△ABM与△CDN中,$\left\{\begin{array}{l}{AM=CN}\\{∠BAM=∠NCD}\\{AB=CD}\end{array}\right.$
∴△ABM≌△CDN(SAS)
(2)∵四边形ABCD是平行四边形,M,N分别是AD,BC的中点,
∴AM=CN,且AM∥CN,
∴四边形AMCN是平行四边形,
∴AN∥CM,
又∵∠BMC=90°,
∴AN⊥BM,
∵易证四边形ABNM是平行四边形,
∴OA=ON,即:点A与点N关于直线BM对称,
∴当点P与点M重合时,△PND的周长最小,
由(1)知:
即:△PND的周长的最小值=△MND的周长=$\frac{5}{2}$+$\frac{5}{2}$+3=8.
点评 本题考查了轴对称-最短路线问题、全等三角形的判定与性质、平行四边形的性质,解题的关键是掌握以上各知识点,证明点A与点N关于直线BM对称是难点.

练习册系列答案
相关题目
15.△ABC中,AB=AC,∠A=∠C,则△ABC是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 不等边三角形 | D. | 不能确定 |
2.水利勘察队沿一条河向上游走了5.5千米,又继续向上游走了4.8千米,然后又向下游走了5.2千米,又向下游走了4.1千米,这时勘察队在出发点的( )处.
| A. | 上游1千米 | B. | 下游9千米 | C. | 上游10.3千米 | D. | 下游1千米 |
17.某校组织学生开展植树活动.为了解全校学生的植树情况,学校随机抽查了20名学生的植树数量,并将调查数据整理如表:
请根据表格提供的信息回答下列问题:
(1)调查的植树数量的众数是2棵;
(2)求这20名学生的植树数量的平均数;
(3)若该校共有500名学生,请根据调查的数据估计该校学生的植树总数约是多少棵?
| 植树数量(单位:棵) | 1 | 2 | 3 | 4 | 5 |
| 人数(单位:人) | 4 | 8 | 4 | 2 | 2 |
(1)调查的植树数量的众数是2棵;
(2)求这20名学生的植树数量的平均数;
(3)若该校共有500名学生,请根据调查的数据估计该校学生的植树总数约是多少棵?
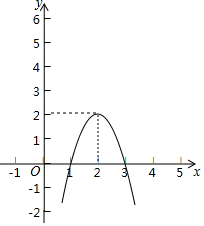 如图,二次函数y=-2(x-2)2+2的图象.
如图,二次函数y=-2(x-2)2+2的图象.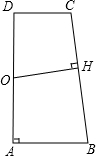 如图,在梯形ABCD中,AB∥DC,∠A=90°,AB=4,CD=3,BC=7,O为AD边的中点,则点O到BC的距离为2$\sqrt{3}$.
如图,在梯形ABCD中,AB∥DC,∠A=90°,AB=4,CD=3,BC=7,O为AD边的中点,则点O到BC的距离为2$\sqrt{3}$.