题目内容
17. 甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过15小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地100千米.
甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过15小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地100千米.
分析 当x=0时,y=300,故此可得到AB两地的距离为300,3小时后两车相遇,从而可求得两车的速度之和,然后依据5小时后两车的距离最大,可知甲车到达B地用5小时,从而可乙车的速度,由图象可知甲车到达B地的时间,从而知道乙车5小时行驶的路程,继而得出答案.
解答 解:由图象可得:当x=0时,y=300,
∴AB=300千米.
∴甲车的速度=300÷5=60千米/小时,
又∵300÷3=100千米/小时,
∴乙车的速度=100-60=40千米/小时.
由图象可知当x=5时,甲车到达B地,
此时乙车行驶的路程为5×40=200(千米),
∴乙车距离A地100千米,
故答案为:100.
点评 本题以行程问题为背景的函数图象的应用,解决问题的关键是根据函数图象理解题意,求得两车的速度.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
7.在三角形的角平分线、中线、高线中,属于直线的有(每种线只有一条)( )
| A. | 0条 | B. | 1条 | C. | 2条 | D. | 3条 |
7.对一批衬衣进行抽检,统计合格衬衣的件数,得到合格衬衣的频数表如表:
估计任抽一件衬衣是合格品的概率0.95.
| 抽取件数(件) | 50 | 100 | 200 | 500 | 800 | 1000 |
| 合格频数 | 47 | 93 | 189 | 489 | 760 | 950 |
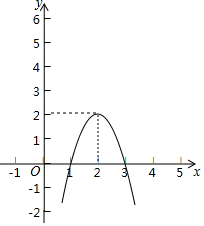 如图,二次函数y=-2(x-2)2+2的图象.
如图,二次函数y=-2(x-2)2+2的图象. 如图是一个长方形推拉窗,窗高1.5米.当活动窗扇拉开长度b(米)时,长方形窗框的通风面积为1.5b米2.
如图是一个长方形推拉窗,窗高1.5米.当活动窗扇拉开长度b(米)时,长方形窗框的通风面积为1.5b米2.