题目内容
2.计算:(1)$5\sqrt{2}-7\sqrt{12}-4\sqrt{\frac{1}{8}}$
(2)3$\sqrt{2}$×$\frac{1}{2}$$\sqrt{6}$÷$\sqrt{8}$
(3)$-{(\frac{3}{{\sqrt{2}}})^2}-\frac{1}{3}\sqrt{8}+{({\sqrt{3}-1})^0}+{2^{-1}}$.
分析 (1)先对原式化简,再合并同类项即可解答本题;
(2)先对原式化简,再合并同类项即可解答本题;
(3)根据幂的乘方、零指数幂、负整数指数幂先对原式化简,再合并同类项即可解答本题.
解答 解:(1)$5\sqrt{2}-7\sqrt{12}-4\sqrt{\frac{1}{8}}$
=$5\sqrt{2}-14\sqrt{3}-\sqrt{2}$
=4$\sqrt{2}-14\sqrt{3}$;
(2)3$\sqrt{2}$×$\frac{1}{2}$$\sqrt{6}$÷$\sqrt{8}$
=$3\sqrt{2}×\frac{\sqrt{6}}{2}×\frac{1}{2\sqrt{2}}$
=$\frac{3\sqrt{6}}{4}$;
(3)$-{(\frac{3}{{\sqrt{2}}})^2}-\frac{1}{3}\sqrt{8}+{({\sqrt{3}-1})^0}+{2^{-1}}$
=$-\frac{9}{2}-\frac{2\sqrt{2}}{3}+1+\frac{1}{2}$
=-3-$\frac{2\sqrt{2}}{3}$.
点评 本题考查二次根式的混合运算、零指数幂、负整数指数幂,解题的关键是明确各自的计算方法,仔细认真化简,会合并同类项.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
14.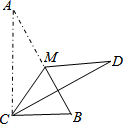 如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
 如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
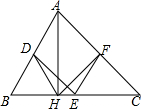 已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.
已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.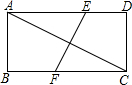 如图,矩形ABCD中,AB=2,AD=4,AC的垂直平分线EF交AD于点E,交BC于点F,则DE=$\frac{3}{2}$.
如图,矩形ABCD中,AB=2,AD=4,AC的垂直平分线EF交AD于点E,交BC于点F,则DE=$\frac{3}{2}$.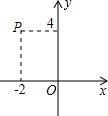 点P在平面直角坐标系的位置如图所示,将点P向下平移a个单位得点P′,若点P′到x轴和y轴的距离均相等,且点P′在第三象限,则a的值是6.
点P在平面直角坐标系的位置如图所示,将点P向下平移a个单位得点P′,若点P′到x轴和y轴的距离均相等,且点P′在第三象限,则a的值是6.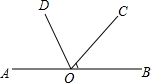 如图,点O在直线AB上,∠BOC=40°,OD平分∠AOC,求∠BOD的度数.
如图,点O在直线AB上,∠BOC=40°,OD平分∠AOC,求∠BOD的度数.